From the Big Bang, to Atoms, to Galaxies to Humans to AI. Entropy & the Arrow of complexity

Abstract

Abstract: This thesis explores the hypothesis that complexity in the universe tends to increase over time, not only in biological systems but also in nonliving systems. We integrate perspectives from physics, astrobiology, evolutionary biology, and philosophy of science to argue that there is a directional trend—an “arrow of complexity”—complementing the arrow of entropy. We examine functional information as a quantitative measure of complexity and discuss how iterative selection processes, analogous to natural selection, operate in domains beyond biology. We propose that a law of increasing functional information may represent a new fundamental principle, consistent with known physics yet highlighting the role of selection in driving evolution . Sudden “phase transitions” in complexity (e.g. the origin of life, multicellularity, cognition) are analyzed as critical points where new emergent rules and functions redefine what counts as complex. We explore how context and functionality determine complexity, noting that as systems evolve, novel functions and contexts co-evolve. The thesis also delves into the epistemological implications of open-ended, self-referential evolutionary processes, drawing analogies to Gödel’s incompleteness (i.e., no fixed formal system or encompass the unbounded emergence of novelty in evolution). Expanding possibility spaces allow new structures and laws to emerge (“more is different”), suggesting that higher-level complexities are not reducible to initial conditions alone. Finally, we discuss implications for astrobiology and consciousness: if complexity’s increase is universal, life and intelligence may be common outcomes of cosmic evolution, and consciousness might be understood as a high-level manifestation of complex information integration. Keywords: complexity, functional information, selection, emergence, entropy, astrobiology, open-ended evolution, consciousness.

Introduction

The universe has evolved from a hot, uniform primordial state to a cosmos rich with structure: galaxies and stars, diverse chemical elements, planets, and on at least one planet, living organisms capable of reflecting on the cosmos itself. This progression invites a profound question: Does complexity tend to increase over time as a general trend or law of nature? The intuition that there is a progressive buildup of complexity – from quarks to atoms, to molecules, to life, to mind – stands in contrast to the Second Law of Thermodynamics, which dictates an overall increase in entropy (disorder) over time. Yet, we observe that localized pockets of the universe (e.g. Earth’s biosphere) have produced highly ordered, complex systems by dissipating energy to their surroundings, thus obeying the Second Law while carving out pockets of increasing complexity. This apparent paradox between entropy and complexity motivates our investigation.

Background and Hypothesis:

In biological evolution, it has long been debated whether there is an intrinsic drive toward greater complexity. While Darwinian evolution has no predetermined goal, the fossil record shows episodes of increasing organismal complexity (for example, the emergence of multicellular life from unicellular ancestors). Some theorists have proposed that even without adaptive “drive,” a passive tendency exists for complexity to increase over time due to diffusion away from minimal complexity states (McShea’s “Zero-Force Evolutionary Law”). Our hypothesis, however, extends beyond biology: we posit that selection-like processes operating on variations can cause complexity to rise in physical and chemical systems as well. In other words, the same fundamental ingredients – variation, differential persistence, and accumulation of information – may underpin a general complexification of matter and energy in the universe.

Scope and Aims:

This thesis seeks to rigorously explore the idea of a universal trend of increasing complexity. We will examine concepts of functional information (a measure of info (Consciousness, complexity, and evolution - PubMed)chieves specific functions) as a unifying metric for complexity in both living and nonliving systems. We will ask whether there could be a new law of nature analogous to the laws of thermodynamics that encapsulates this complexification tendency. Key themes include the role of selection processes (broadly construed) in driving complexity, the importance of context and function in defining what is complex, and the occurrence of major transitions or phase changes where complexity jumps discontinuously. We will also tackle the philosophical implications of open-ended evolution – in which there is no final “highest” complexity because new possibilities keep emerging – and the limits of formal reducibility of such processes (drawing parallels to Gödel’s incompleteness theorem). Finally, we will discuss what an “arrow of complexity” might mean for predicting the presence of life elsewhere in the universe and for understanding consciousness as a phenomenon of organized complexity.

Structure:

The thesis is organized as follows. In the Literature Review, we survey existing research on complexity in cosmology, biology, and information theory, including attempts to quantify complexity and previous arguments for or against an intrinsic directionality in evolution. The Theoretical Framework chapter defines key concepts – entropy versus complexity, various complexity metrics, functional information, and generalize (How much consciousness is there in complexity? - Frontiers)– that will be used in our analysis. The Core Arguments are presented in several chapters, each tackling one aspect of the central hypothesis: (1) functional information’s role in evolution, (2) the universality of selection processes beyond biology, (3) complexity as a directional arrow of time, (4) a possible new law of complexification in analogy to thermodynamics, (5) the evolving nature of function and context in complexity, (6) sudden jumps in complexity and major transitions, (7) the epistemological implications of self-referential open-ended systems (with Gödelian analogies), and (8) expanding possibility spaces and emergent new rules. We then turn to Implications and Predictions, where we speculate on the future trajectory of complexity on Earth and in the cosmos, and how this framework guides the search for extraterrestrial life and an understanding of consciousness. In Limitations and Open Questions, we critically assess the hypothesis, addressing potential counterarguments (e.g. periods of decreasing complexity, or alternative explanations) and identifying what remains uncertain. Finally, the Conclusion summarizes our findings and suggests directions for future research into the laws of complexity.

By integrating knowledge across disciplinary boundaries, this work aims to synthesize a coherent argument that complexity’s increase is not an accidental byproduct confined to biology, but rather a fundamental, unifying process in nature – one that complements the increase of entropy and might guide us toward new principles in science.

Literature Review

Complexity in Physical and Biological Systems

Evolution of Complexity in Cosmology:

From a cosmological perspective, the universe’s history can be seen as a series of emergent complex structures. After the Big Bang, the nearly uniform plasma gave way to atoms (simple structures), which then gravitated into stars and galaxies, enabling nucleosynthesis of heavier elements. Those elements formed planets and, on at least one planet, combined into self-replicating molecules and living cells. Astrophysicist Eric Chaisson has quantitatively argued that complexity has risen over cosmic time by analyzing the energy flow through systems. He introduced a metric called free energy rate density (energy flow per unit mass), finding that this metric correlates with intuitive complexity: galaxies have higher energy rate densities than diffuse gas, stars higher than galaxies, planets higher than stars, living cells higher than planets, and human brains higher than simple cells. Chaisson’s data, plotted over ~14 billion years of cosmic evolution, show an overall exponential increase in this complexity metric from the Big Bang to the present. While entropy of the universe as a whole increases, these results suggest that pockets of the universe (open systems far from equilibrium) can and do become more complex by utilizing energy gradients. In Chaisson’s words, “energy flow as a universal process helps suppress entropy within increasingly ordered, localized systems…in full accordance with the second law of thermodynamics” – no known physical laws are violated by local increases in order, because greater disorder (heat) is dumped into the environment.

Evolution of Complexity in Biology:

Biological evolution provides the most well-studied example of increasing complexity. Over Earth’s history, life has diversified from relatively simple single-celled organisms to extremely complex multicellular organisms and ecosystems. Theoretical biologists John Maynard Smith and Eörs Szathmáry famously catalogued the Major Transitions in Evolution – landmark events such as the origin of replicating molecules, the emergence of chromosomes, the origin of the genetic code, the evolution of eukaryotic cells (with organelles), the evolution of multicellularity, the origin of societies, and language. Each transition represented smaller units coming together to form larger, more complex units with new types of information flow (e.g., from single genes to chromosomes, or from single-celled organisms to multicellular ones). These transitions illustrate how complexity sometimes increased in jumps rather than a smooth continuum. They also show that what counts as a unit of selection can change – for instance, once independent cells become integrated into a multicellular organism, the “organism” becomes the new unit of selection, leading to a new level of complexity.

Debate exists in evolutionary theory about whether complexity’s increase is an inherent trend or a passive result of random variation. Stephen Jay Gould argued that the appearance of a trend toward complexity can arise simply because there is a lower bound on simplicity (you can’t get much simpler than a bacterium), so over time variance will spread out and some lineages will become more complex even without any directional pressure (“drunkard’s walk” model). In contrast, Daniel McShea and Robert Brandon proposed a “Biology’s First Law” – that in the absence of constraints, complexity (measured as differentiation of parts) will tend to increase spontaneously (a passive trend). Empirical work by McShea and others found that, indeed, over geological time the maximum complexity of organisms tends to increase, although the mode or average might not (many organisms remain simple). Thus, there is evidence for an overall envelope of increasing maximal complexity, even if not all lineages become more complex.

Quantifying Complexity:

A challenge in these discussions is defining and quantifying “complexity.” Different metrics exist, each capturing different intuitions:

• Shannon entropy measures information as uncertainty or disorder, but a high-entropy string (random noise) is typically not what we mean by complex organization.
• Algorithmic (Kolmogorov) complexity measures the length of the shortest program to produce an object. Random noise has high Kolmogorov complexity (no short description), whereas a crystal’s repeating pattern has low complexity. However, algorithmic complexity alone doesn’t distinguish meaningful organization from randomness.
• Effective complexity (proposed by Murray Gell-Mann) attempts to measure the length of a description of the regularities of an object (ignoring random noise) – in theory capturing the structured, non-random aspect that makes something like a living cell more complex than dust.
• Physical complexity (proposed by Seth Lloyd and others) might measure the amount of information a system stores about its environment or past (e.g., how much data is embodied in an organism’s structure).
• Functional information is a particularly useful concept for evolving systems: it measures the amount of information required for a system to achieve a specific function above a given performance threshold. Developed by Robert Hazen and colleagues, this metric explicitly ties complexity to function. For example, among all possible random polymer sequences, very few will fold into a protein that performs a specific job (catalyzing a reaction). Those sequences that do have high functional information relative to that function because a lot of information is needed to specify them out of the combinatorial universe of possibilities. Functional information is measured in bits as I(Ex)=−log⁡2[F(Ex)]I(E_x) = -\log_2 [F(E_x) ], where F(Ex)F(E_x) is the fraction of configurations that achieve at least a given level of funct (Why Everything in the Universe Turns More Complex | Quanta Magazine)L31-L40】. The more demanding the function (higher ExE_x), the smaller F(Ex)F(E_x) is, and thus the higher the information required. This concept will be central to our analysis, as it provides a way to quantify complexity in both living and nonliving systems in terms of what they do (their function) rather than just their microscopic description.

Nonliving Complex Systems and Self-Organization:

Outside of biology, researchers in complexity science have noted many cases of spontaneous ordering in physical and chemical systems. Dissipative structures, a term from Ilya Prigogine, refer to ordered patterns that emerge in systems driven far from equilibrium by energy flow – classic examples include convection cells (Bénard cells) in a heated fluid and the beautiful regularity of a chemical oscillation (Belousov-Zhabotinsky reaction). These structures are temporary and local, but they show that increase in order can naturally occur in nonliving systems given a constant throughput of energy. Similarly, in chemistry, we see self-assembly processes: molecules can spontaneously form organized structures (like lipid membranes or crystals) under the right conditions. While these examples are not increasing complexity indefinitely, they hint at how natural processes can create pockets of order.

One interesting example at a geological scale is mineral evolution. Hazen and collaborators documented that the diversity of minerals on Earth increased dramatically over geological time: early Earth had maybe a couple of dozen types of minerals, whereas today thousands are known. This increase was driven by chemical and environmental changes (e.g., oxygenation enabling new oxides, biological activity creating biominerals). It was not random: each stage of mineral diversification built upon the previous, as new minerals formed in new environments (water-mediated weathering, high-pressure mantle environments, etc.). One can view this as a non-biological complexity increase (in terms of information needed to specify mineral structures, or simply count of distinct solids) driven by planetary evolution. Mineral evolution has even been framed in selecti (On the roles of function and selection in evolving systems | PNAS)inerals that are stable under Earth’s surface conditions “survive” while others transform, implying an analog of selection for persistence of certain crystal structures. Although minerals do not reproduce, the concept of stability under environmental pressures plays a similar filtering role.

Universality of Evolutionary Principles:

Several thinkers have speculated that Darwinian principles might extend beyond biology. The idea of “Universal Darwinism,” introduced by Richard Dawkins and further developed by others like Donald Campbell, suggests that whenever you have systems that replicate with variation and differential success, you will get an evolutionary process leading to adaptation. This has been invoked in contexts such as the immune system (clonal selection of antibodies), cultural evolution (memes), and even cosmic evolution. For instance, physicist Lee Smolin proposed a controversial idea of cosmological natural selection – universes might reproduce via black holes, with slightly different physical constants, and those universes that make more black holes “reproduce” more, suggesting a selection at the multiverse level. While highly speculative, it shows the temptation to see analogies between biological evolution and other domains.

What is emerging from all these studies is a picture that complexity can increase under the right conditions in many systems, and that some general principles – especially the combination of generation of diversity and some kind of selection mechanism – may underlie this increase. However, until recently, no one had formulated a concise “law” for this, analogous to the laws of motion or thermodynamics. Most scientists considered the rise of complexity as a result of many contingent processes rather than a fundamental principle. This thesis, as previewed above, examines a bold proposal that a law-like statement might indeed capture the essence of evolving complexity across biology and physics: the law of increasing functional information. Before developing that argument, we will establish the theoretical framework needed to articulate it clearly.

Complexity, Entropy, and the Arrow of Time

A crucial part of the background is understanding how a directional increase in complexity can coexist with, and indeed be facilitated by, the Second Law of Thermodynamics – the traditional “arrow of time.” The Second Law states that in an isolated (closed) system, entropy (disorder) never decreases; in fact, it increases in any spontaneous process. This law underpins why certain processes are irreversible (e.g. you can’t unmix milk from coffee or cause heat to flow from cold to hot spontaneously). At first glance, the Second Law seems to imply that order and complexity should give way to disorder over time, not increase. How then can galaxies, organisms, and minds arise?

The resolution lies in the fact that Earth, and other systems where complexity grows, are not isolated systems. They are open systems that exchange energy and matter with their environment. Earth receives low-entropy (high-quality) energy from the sun (mostly visible light) and radiates away higher-entropy (lower temperature) energy to space (infrared). This flow essentially allows Earth to export entropy to space, while locally building up order. As physicist Erwin Schrödinger noted in What is Life? (1944), organisms “feed on negative entropy” – they maintain and increase their internal order by exporting entropy to their environment. In thermodynamic terms, the entropy decrease associated with forming a complex structure is offset by a larger entropy increase in the surroundings (often as waste heat). Thus, there is no conflict with the Second Law; rather, the Second Law drives a lot of these processes: systems tend to evolve to dissipate energy gradients, and in doing so they often form complex structures (a concept related to the idea of maximum entropy production principle).

Some researchers have posited that this tendency to form dissipative structures could itself be viewed as a law-like behavior. For example, astrophysicist Chaisson (cited above) argued that the increase in complexity is natural in an expanding, energy-diverse universe. Lineweaver and Egan (2008) explored how life and complexity are consistent with thermodynamics, even suggesting that gravitational clumping (which creates stars and planets – low entropy configurations locally) is an entropy-increasing process overall when you include the generated heat. They phrased it as: entropy (disorder) can increase globally while complexity increases locally, thanks to energy flows.

Philosopher-scientist Sir Julian Huxley in the mid-20th century and Jesuit paleontologist Pierre Teilhard de Chardin earlier had envisioned an evolutionary cosmology where complexity (and consciousness) increase in a quasi-teleological way. Teilhard even suggested a “Law of Complexity-Consciousness” in which increasing material complexity eventually produces higher levels of consciousness – though his ideas were more mystical and not framed in testable scientific terms. Those early ideas set a stage for thinking big about complexity, but modern science requires empirical measures and mechanisms, which is what this thesis emphasizes.

In summary, the literature indicates that:

• The universe’s history provides numerous examples of complexity emerging and growing.
• There is no consensus “law” of complexity, but multiple lines of evidence and theory point toward common principles (like energy flows and selection processes) enabling complexity to rise.
• Any such increase does not violate thermodynamics; rather it relies on thermodynamics in open systems.
• Major transitions in evolution mark significant jumps in complexity, often associated with innovation in information storage/transmission.
• A quantitative handle on complexity that spans physics and biology has been elusive, but concepts like functional information and assembly theory (discussed later) are promising bridges.

These points set the stage for our theoretical framework: we need to formalize what we mean by complexity increase, identify the mechanisms (with selection as a prime suspect), and ensure consistency with fundamental physics. The next chapter develops this framework.

Theoretical Framework

In this chapter, we establish definitions and concepts that will be used throughout our analysis. We clarify what is meant by complexity, functional information, and selection, and describe how these concepts can apply across different domains (physical, chemical, biological, cultural). We also outline the notion of an evolutionary process in a general sense, and how it might generate increasing complexity. Finally, we distinguish complexity from entropy and articulate the conditions under which complexity can increase (open systems driven far from equilibrium).

Defining Complexity and Functional Information

Complexity:

We define complexity, in a general sense, as the degree of structured heterogeneity in a system – that is, how intricate and non-random the arrangement of a system’s parts is. This definition is intentionally broad, as complexity can manifest in many ways (the intricate folding of a protein, the wiring diagram of a brain, the hierarchical structure of a galaxy cluster, etc.). We refine this broad notion by focusing on functional complexity: the complexity relevant to a system’s function or behavior. A random pile of rubble may be geometrically complex, but if it accomplishes nothing, one could argue it’s “organized complexity” that matters more for our purposes (as in Herbert Simon’s definition of complexity relating to how components are organized for some purpose).

Functional Information (FI):

Proposed by Hazen et al. (2007), functional information is a quantitative measure tailored to the idea of function or performance. For a given system and a specified function (with a performance threshold), FI measures how improbable it is to achieve that function by chance. Formally, if NtotalN_{total} is the total number of possible configurations of the system (e.g., all possible sequences of amino acids of a certain length), and N(Ex)N(E_x) is the number of configurations that achieve at least a level ExE_x of performance at the function, then F(Ex)=N(Ex)/NtotalF(E_x) = N(E_x)/N_{total} is the fraction of configurations that meet or exceed that function level. The functional information is defined as I(Ex)=−log⁡2[F(Ex)]I(E_x) = -\log_2 [F(E_x)]. If only 1 in a million configurations can do the function, II is about 20 bits (since 220≈1062^{20} \approx 10^6). If 1 in 2 can do it (a trivial function many configurations satisfy), II is 1 bit. FI is thus high for systems that are highly specified to achieve a function.

A crucial aspect of FI is that it is context-dependent and function-dependent. The same physical configuration can have high FI with respect to one function and zero with respect to another. For example, a hammer has high FI for pounding nails (few random objects can do that well), but near zero FI for, say, absorbing water (many materials can absorb water, a hammer cannot – but we wouldn’t consider that its function). Hazen et al. emphasize that FI must be defined relative to a chosen function and environment, but that doesn’t make it subjective – one can objectively state the function and measure performance. The maximum FI of a system is achieved when only a single configuration accomplishes the function to the highest degree, essentially encoding all bits of the configuration as functional requirements. The minimum FI is zero, when a function is so easy that even random configurations can do it (or no configuration can do it at all).

Why use functional information? Because it directly ties the idea of complexity to something that matters for the system’s propagation or stability. Biological evolution cares about functional complexity (e.g., a slight change in DNA that improves an enzyme’s function can be selected for). In nonliving systems, we can analogously think in terms of function: for instance, in a star, one might say the “function” is fusing hydrogen (or simply persisting in hydrostatic equilibrium); only certain configurations of mass/pressure/temperature profile achieve that stable star state – we could talk about FI associated with stellar stability. In mineral evolution, the “function” might be being a thermodynamically stable mineral under certain conditions. Hazen’s concept essentially allows us to quantify how special or rare a configuration is given a functional criterion, which correlates with what we intuitively call complexity or specificity.

Throughout this thesis, when we speak of complexity increasing, we often mean that the functional information content of systems is increasing. For example, the first replicating RNA molecule on Earth had some functional information (relative to the function of self-replication), but today’s DNA-polymerase-and-ribosome-based replication system has astronomically more FI with respect to precise self-reproduction and metabolism. That increase in FI corresponds to a huge increase in complexity required for life’s functions.

Generalized Selection and Evolutionary Processes

Selection:

In biology, natural selection is the differential survival and reproduction of entities (organisms or genes) based on her (On the roles of function and selection in evolving systems | PNAS)ion in traits. A key insight of this thesis is that selection in a broader sense can occur in systems that are not strictly biological reproduction. We define selection in a generalized way: any process by which some configurations of a system preferentially persist or proliferate over others, due to some criterion (which we can call a function or fitness). Selection requires a mechanism to generate or present variation (different configurations) and a mechanism to choose among them based on performance at some function (which could be as simple as stability under given conditions).

Hazen et al. (2023) identify three universal concepts of selection applicable to various systems:

• Static persistence: some configurations just last longer (are more stable) than others. (In a chemical system, a more stable molecular arrangement might persist while others break down.)
• Dynamic persistence: some configurations are generated or replenished at higher rates. (In an ecosystem, rabbits reproduce faster than elephants, for example.)
• Novelty generation: processes that create new configurations (mutations, innovations, recombination).

Together, these ensure that out of a huge space of possibilities, some subset comes to dominate the population of configurations as time goes on. Whether that population is “molecules in a test tube,” “mineral species on Earth,” or “organisms in an ecosystem,” the idea is similar.

Hazen and colleagues have boldly proposed a “Law of Increasing Functional Information”: The functional information of a system will increase over time (i.e., the system will evolve) if many different configurations of the system undergo selection for one or more functions. This law is meant to parallel other natural laws by identifying a parameter (functional information) that universally tends to increase under certain conditions. Notably, this law doesn’t say complexity must always increase; it gives a condition – presence of variation and selection for function – under which complexity will increase. It’s essentially generalizing Darwin’s insight: selection inexorably accumulates adaptations (which are functional information).

For this law to hold outside biology, we need to recognize selection-like dynamics in other realms:

• In stars: Among many possible dispersal of matter, only certain configurations form long-lived stars. One can say gravity “selects” clumps of matter that are able to initiate fusion and withstand pressure. Those configurations persist (stars shine for billions of years), while others (random gas dispersions) do not form bound structures and thus “fade away.” Over cosmic time, matter has been increasingly found in forms that are locally more complex (stars, planets) because simpler distributions (homogeneous gas) are unstable and collapse – a kind of selection for gravitationally bound states.
• In chemistry: If we start with simple molecules and provide energy, we might get a host of products, but the ones that accumulate are those that are stable (static persistence) or those autocatalytically produced (dynamic persistence). This is chemical selection. Over time, more complex molecules that are stable in the environment can build up (like a network of organic reactions on the early Earth leading to the first replicators).
• In technology or culture: Ideas, inventions, and designs undergo selection in human society – useful ones spread, useless ones are discarded. This has led to increasing complexity in culture (compare technology today vs. the Stone Age). Although guided by intelligence, the cumulative evolution of technology has parallels with biological evolution (variation generated by inventors, selection by markets or utility, retention of improvements).

*Arrow of Time (On the roles of function and selection in evolving systems | PNAS) (On the roles of function and selection in evolving systems | PNAS) Selection processes impart an arrow of time because they are inherently historical and path-dependent. Once a particular complex configuration is reached (e.g., a DNA-protein world in biology), the system’s future possibilities are constrained and enabled by that history. This is a (On the roles of function and selection in evolving systems | PNAS) (On the roles of function and selection in evolving systems | PNAS)lution is a history-dependent process – you can’t generally reverse it and you can’t skip intermediate steps easily. The configurations that exist today (like modern cells) carry a record of past selections (Why Everything in the Universe Turns More Complex | Quanta Magazine) (Why Everything in the Universe Turns More Complex | Quanta Magazine)his irreversibility is analogous to thermodynamic irreversibility. In fact, one could say there are twin arrows: entropy’s arrow (increasing entropy) and complexity’s arrow (increasing functional information). They are not contradictory but complementary: entropy’s arrow provides the overall direction and energy dissipation required, while complexity’s arrow traces the specific pathways where entropy production has been harnesse (Microsoft Word - Georgiev ECCS14 7.23.15 rev2 For Arxiv) ()32-L339】.

Emergence, Context, and Levels of Organization

*Emergent Rules: Complexity increases to a new level, we often get new “rules” or principles that govern that level. This is the concept of emergence, famously captured by Nobel physicist P. W. Anderson’s phrase “More is Different”. For example, when individual neurons form a network, new phenomena emerge (like memory, computation) that are not properties of single neurons in isolation. The emergent laws (e.g., psychology or network dynamics) don’t contradict physical laws but are additional, higher-level descriptions. In our context, as complexity grows, the context in which parts operate changes. The same molecule might behave differently within a complex cell than in a dilute solution because the cell provides scaffolding, energy fluxes, and other interactions – effectively a new context that can give the molecule a function. Thus, function is context-dependent: what counts as useful or complex is defined with respect to the environment and system.

This means our measure of complexity (functional information) can itself evolve as context changes. Early in evolution, a simple repl (The Major Transitions in Evolution - Wikipedia)function might just be to make more of itself. Later, in a cell, that RNA might become part of a ribosome and its function is in translation. Its complexity in the new context is judged by new criteria. Therefore, one must keep track of the evolving definition of function. We will see in the core arguments how context shifts (e.g., new levels of (No entailing laws but enablement in the evolution of the biosphere')ike multicellular life or technological ecosystems) alter the landscape of complexity.

Open-Ended Evolution and Incompleteness:

A system exhibits open-ended evolution if it can keep producing novel forms or functions without a known limit. Life on Earth appears to be open-ended in this sense – new species, new biochemicals, new behaviors continue to arise. In contrast, something like a crystal-forming system reaches a limit (once the crystal is formed, (Study: "Assembly Theory" unifies physics and biology to explain evolution and complexity | Santa Fe Institute) (Assembly theory explains and quantifies selection and evolution | Nature)es). One intriguing framework to understand this concept is in terms of possibility spaces. As complexity increases, the space of achievable configurations often expands, because new combinations become reachable. Stuart Kauffman introduced the idea of the adjacent possible – at any state, there is a set of novel states one step away that were not previously accessible; as you move into one of those, new adjacent possibles appear, expanding the frontier. This leads to a combinatorial explosion of what can happen, given enough diversity and time.

Mathematically, one can’t necessarily pre-compute all possible emergent features because they depend on context and higher-order interactions. This resonates with Gödel’s incompleteness in a metaphorical way: G (Consciousness, complexity, and evolution - PubMed)at any formal axiomatic system capable of arithmetic is incomplete – there are true statements it cannot prove. By analogy, any fixed description of an evolving system will eventually be “incomplete” to describe new patterns that emerge. No finite set of rules can entail all future innovations of an open-ended evolving system. Kauffman and others have argued that there are “no entailing laws” fully dictating the evolution of the biosphere; instead, evolution is a process where new possibilities (and new “laws” at higher levels) keep coming into being. This doesn’t violate physical laws; it means that to predict evolution, listing physical laws isn’t enough – you’d need to somehow foresee novel functional (On the roles of function and selection in evolving systems | PNAS)will emerge, which is in principle as h (On the roles of function and selection in evolving systems | PNAS)ematical system trying to produce a stateme (On the roles of function and selection in evolving systems | PNAS) (On the roles of function and selection in evolving systems | PNAS)y.

**Levels of Selection and Indivi (Study: "Assembly Theory" unifies physics and biology to explain evolution and complexity | Santa Fe Institute)complexity grows, often new levels of individuals arise: genes -> cells -> multicellular organisms -> societies, etc. At each level, selection can act (e.g., selection among organisms in a population). For complexity to further increase, cooperation and integration at a lower level must occur so that higher-level entities can emerge (Maynard Smith and Szathmáry emphasized this). There is often a tension between levels – e.g., a cell in a multicellular body could “rebel” (cancer) which is a breakdown of integration. So, a system must evolve governance mechanisms to maintain the new higher level. This is part of the evolving context: what was a freely reproducing cell becomes constrained as part of an organism. But the organism can do things (functions) that single cells cannot, thus unlocking new complexity (like having organs, nervous systems, etc.).

A Possible New Law of Nature?

We now formalize the conjecture mentioned: Could there be a law of nature governing the increase of complexity, analogous in stature to other laws (while, of course, consistent with them)? Hazen, Walker, and colleagues (PNAS 2023) suggest precisely this: If a system has the capacity to explore many configurations and there is selection for function, then functional information tends to increase. In formulaic terms, d(FI)/dt > 0 under those conditions. They compare it to how the Second Law is statistical (entropy tends to increase in closed systems) – here it’s an evolutionary law (functional complexity tends to increase in open, selected systems).

It’s important to test this idea against known examples. Does it hold that functional information increases? In evolutionary experiments, yes – for instance, experiments with digital organisms or RNA molecules show that with mutation and selection, functional efficacy improves over generations, corresponding to higher FI to meet that function. Hazen et al. performed simulations where simple algorithms mutated and competed, and indeed the functional information (relative to a computational task) increased spontaneously over time. In chemistry, one could imagine an experiment where a mixture of polymers is subject to some selection (say binding to a target); over cycles of selection and reproduction (like SELEX experiments for aptamers), the information content of the polymers binding the target increases – this is essentially directed evolution and is routinely observed in the lab. These are evidence that the “law” holds in those scenarios.

One must also consider if there are limits or exceptions. Could FI ever decrease? In principle, if the selection pressures relax or change, complexity might decrease (e.g., parasites often simplify genomically when they start relying on a host – they lose functions that are no longer needed, a kind of reverse complexity). However, the law is stated for when selection for function is present. If the environment no longer selects for a complex function, that function’s associated complexity can dwindle (atrophy of unused traits). So the law would apply chiefly during periods of sustained selection for certain (or new) functions. Additionally, selection can drive simplification if simplicity is favored (some environments favor smaller genomes or fewer parts). Thus, a refined statement might be: functional information of a system tends to increase up to the point that efficiency or adaptation requires simplicity. In practice, evolution often produces a mix of increases and decreases in complexity depending on what is advantageous. But across multiple traits and over long periods, the envelope of what has been achieved keeps expanding.

In summary, our theoretical framework posits that increasing complexity is driven by a combination of:

• Energy flow (to enable local entropy reduction and work against disorder).
• Variation generation (to explore many possible configurations).
• Selection for function (to preferentially retain the more functional/organized configurations, thereby accumulating functional information).
• Emergent stabilization (new structures creating new contexts that allow further complexity to build without falling apart).
• Historical contingency (the path-dependent accumulation, making the process effectively irreversible and open-ended as new possibilities emerge).

With these concepts defined, we can now proceed to the core arguments, examining the pieces of our hypothesis in detail and supporting them with evidence and logical reasoning.

Core Arguments

Functional Information as the Currency of Complexity in Evolution

A central claim of this thesis is that functional information (FI) is the “currency” by which complexity grows in evolving systems. This means that as systems become more complex, what is really increasing is the amount of information specifying configurations that achieve certain functions. In biological terms, evolution encodes information about how to survive and reproduce (functions) in genomes and structures; over time, the information content required for those functions accumulates. In non-biological terms, we can speak of information being embedded in physical structures that allow them to persist or perform certain processes.

FI in Biological Evolution:

Every adaptive trait in an organism (e.g., the camera-eye of vertebrates, the flight mechanism in birds) carries functional information – it is a solution to a problem (seeing, flying) that out of many random configurations, only specific complex arrangements solve. The evolution of such a trait is essentially the increase of FI in the lineage’s genome. Early in eye evolution, perhaps a simple light-sensitive patch was present (low FI for basic light detection). Over time, through selection, more information was added: genes for lenses, for an iris, for image processing, etc. The fully developed eye has much higher FI relative to the function of high-resolution vision than the initial light spot. This increase occurred stepwise with each beneficial mutation adding bits of information (in the sense of reducing the space of possibilities to hone in on ones that work better).

Hazen and Szostak’s work put numbers to this idea using simpler model systems. For example, they considered short protein-like polymers and a target function (binding a particular molecule). If one starts from random sequences (which have low probability of binding well, hence high FI required to achieve strong binding), and then simulate selection and mutation, one observes the average functional information of the population increases generation by generation. In one simulation, random “digits” were evolving to perform arithmetic operations; initially their performance was poor (low FI for that function), but as they evolved, their performance approached theoretical maxima, indicating the system discovered configurations (algorithms) that encode the solution – the FI increased spontaneously over time. These simulations mirror natural evolution in principle.

FI in Chemical Evolution (Origin of Life):

Prior to true reproduction, chemical systems might have undergone a kind of selection. The origin of life can be seen as the gradual buildup of functional information in molecular networks until a tipping point was reached where self-sustaining, self-reproducing systems existed. Hazen (as cited in the Quanta article) argued that life versus nonlife is a continuum, with functional information driving the process from simple to complex. The first replicator (perhaps an RNA molecule capable of making copies of itself) had to be selected from a vast space of random polymers – a dauntingly low probability event unless there were chemical pathways guiding it. Some researchers (e.g., Eigen’s hypothesis of a hypercycle) suggest that partial functionalities (like metabolism, compartmentalization, simple templates) accumulated before full self-replication. In each step, FI increased: e.g., a lipid vesicle that can grow and divide has FI regarding that function of compartmentalization; an enzyme that catalyzes a reaction has FI for that reaction.

As life emerged, functional information became concentrated in polymers (nucleic acids and proteins). An interesting perspective is to consider the total functional information on Earth locked in biology. It has certainly increased from zero before life, to whatever astronomical number of bits is encoded in all the DNA sequences, protein structures, and biochemical networks today. Earth’s biosphere is essentially an FI-rich system, containing solutions to countless functional challenges (from photosynthesis to flight to symbiosis).

FI in Nonliving Complex Systems:

It may seem odd to talk about function for nonliving systems, but recall Hazen’s broad definition: function is just what some selection criterion favors. In stars, the “function” we might consider is something like longevity or energy dissipation. A star configuration that dissipates energy steadily for a long time (through fusion) is “selected” by virtue of persistence. We can imagine measuring the FI of different configurations of matter for the function “remain a star for at least 1 million years”. The Sun’s configuration has high FI for that function – random assemblies of gas do not. How did the Sun (and billions of other stars) come about? Through gravitational collapse, which tried many “configurations” (different fragmentations of a gas cloud), but only certain ones satisfied the criteria to ignite fusion and hold together. In that sense, gravity plus thermodynamics performed a selection of long-lived stars from many initial perturbations. Over cosmic time, more FI is stored in structures like stars and planets compared to the smooth initial state of the universe. Each stable structure (planet, star, crystal) contains information – for instance, the precise positions and bonds of atoms in a crystal lattice encode information about the environment in which it formed.

Another example: planetary atmospheres might evolve complexity. One can think of an atmosphere’s chemical network and possible emergence of far-from-equilibrium states (like Jupiter’s Great Red Spot, a persistent vortex – a structure that serves the “function” of a stable storm). Only certain complex flows produce such giant vortices; they emerge and persist because they are stable configurations that dissipate energy (the gradient between Jupiter’s equator and poles, for example). If we quantitated the complexity of Jupiter’s atmosphere over time, it might have increased as the planet settled into patterns (this is speculative, but illustrates how even non-biological planets can have dynamical structures that contain information).

Cumulative Nature of FI:

One significant aspect of functional information is that it tends to be cumulative: complex systems often retain the simpler functionalities as sub-functions. A multicellular organism still has cells that perform basic metabolism, an advanced technology (like a smartphone) still contains basic electronic components that must function properly. Thus, as complexity grows, it layers new FI on top of existing FI. Evolution doesn’t usually erase the old (unless it becomes a burden); it repurposes and adds onto it. This means the total FI of a system can keep growing. However, it also means systems can accrue “information debris” or vestigial parts that no longer serve a function, which may later be lost (this is one way FI can decrease locally).

To use a metaphor: functional information is like knowledge gained by a learning process (here, evolution is the learning algorithm). Just as a human technical knowledge base increases over history (we rarely lose fundamental knowledge, we only add more), the biosphere’s knowledge (DNA) about how to survive in various ways has increased. Occasional loss of information happens (extinctions, simplifying parasites), but the overall pool on the planet has grown (especially with human culture adding another layer of information).

In conclusion of this section, functional information provides a robust way to discuss complexity increase quantitatively. It grounds the abstract idea of “order” in concrete, measurable terms of function and probability. This concept will be used in subsequent sections to argue for a universal selection-driven increase in complexity.

Selection Processes Beyond Biology: A Universal Darwinism

One of the bold assertions we explore is that the Darwinian mechanism of variation and selection is not exclusive to life, but a general algorithm that can occur in many systems, thereby driving complexity outside the biological realm. This idea, sometimes called “universal Darwinism,” extends the principles of evolution to phenomena like chemistry, astrophysics, and even information systems.

Darwinian Algorithm in Abstract:

The core of Darwinian evolution is often summarized as: Replication, Variation, Selection. However, even without strict replication, a similar outcome arises if there is repeated trial and error with retention of successes. We can phrase a generalized Darwinian algorithm:

1. Generate many configurations (states, patterns) of a system (by whatever process – random fluctuations, exploratory moves, etc.).
2. Have a criterion that preferentially keeps some configurations around longer or makes them more likely to be the basis for the next generation of configurations. (This is analogous to selection – the criterion is usually a function or stability measure).
3. Repeat, with modifications or combinations of the retained configurations generating new ones.

Biological evolution fits this perfectly: organisms generate offspring with variations; nature selects those better fitted; repeat over generations. Now, consider other domains:

Chemical Selection:

Before life, chemical reactions in a complex mixture can produce a variety of molecules. If some molecule catalyzes its own formation (an autocatalytic molecule) or is especially stable, it will accumulate relative to others. This is a selection effect. Over time, the mixture’s composition shifts towards molecules that are stable or self-promoting – a primitive evolutionary dynamic. Researchers have created experiments with RNA strands in test tubes (like Spiegelman’s RNA replication experiment) that show selection for faster replicating RNA: even outside a cell, if you provide the machinery (a replicase enzyme) and variation (initial random RNA), the RNAs that happen to replicate fastest will dominate. This is evolution in vitro, and it doesn’t require a “living” organism per se. Similarly, in crystal growth, one might say the crystal structure that best fits the conditions nucleates and grows, whereas other arrangements don’t propagate – the environment “selects” a particular crystal form among possible polymorphs.

Mineral and Stellar “Evolution”:

Hazen et al. have likened processes like mineral diversification to evolution. In mineral evolution on Earth, each stage of mineral formation changed the environment in ways that allowed new minerals to form. For example, once photosynthesis put oxygen into the atmosphere, many new oxide minerals appeared (like iron oxides, giving us red rust layers in geological strata). The phrase “selection” can be used here: the changing environment “selects” which minerals are stable. If a mineral forms that is unstable in oxygen, it will be converted into another (so it disappears, akin to being unfit). Only those mineral species that can persist in the new conditions remain. Over time, more and more mineral species accumulated, in part because new ones didn’t replace all old ones but added to the total in new niches (some pockets with no oxygen still held old minerals, etc.). So diversity and complexity of the mineral ensemble increased. This is analogous to an ecosystem diversifying under varied conditions.

In stellar evolution (the term “stellar evolution” in astrophysics refers to a star’s life cycle, but here we mean population of stars), a giant molecular cloud might fragment into many protostars. Not all survive – some may merge or get disrupted. The ones that achieve stable nuclear fusion and balance will shine as stars for a long time (selected for persistence), whereas others might fizzle out as brown dwarfs or get torn apart. Over multiple generations (massive stars explode as supernovae, seeding new clouds with heavy elements, which then form second-generation stars), one could see a form of iteration. Stars don’t replicate in the way organisms do, but there is a population with variation (different masses, compositions) and differential outcomes (some live longer, some shorter, some produce more offspring like planets or new clouds). One might say the universe “selects” for stars that are good at dispersing energy from collapsing gas (since that’s what they do). The concept of cosmic natural selection proposed by Smolin goes further to speculate that universes might breed via black holes, but even if that is far-fetched, within a universe we see repeated cycles of structure formation with a kind of filtering mechanism – call it selection – at work.

Memetic and Cultural Evolution:

Richard Dawkins coined the term meme for a cultural idea or practice that propagates from mind to mind, analogous to a gene. Memes clearly undergo variation (people modify stories, invent new tunes), and selection (catchy or useful ideas spread; others fade away). The evolution of languages, for example, is an evolutionary process – words and grammatical structures mutate over centuries, and those that are easier or more expressive survive in usage. Although driven by conscious agents, the large-scale pattern is unintentional and Darwinian in character. Cultural evolution has led to increasing complexity of technologies and social systems. Simple stone tools evolved into today’s vast technological ecosystems not by genetic evolution, but by a cultural analogue where human choices provide selection pressures (often favoring more complexity because it can achieve more functions).

In technology, there’s even evolutionary computing: algorithms improve solutions by simulating selection (generating many candidate solutions and selecting the best to “reproduce”). These algorithms have produced innovative designs (like antenna shapes evolved by NASA’s software) that human engineers might not have conceived, demonstrating the general power of selection to create complex, functional designs even outside organic life.

Common Principles:

What unites these examples is differential persistence. Selection doesn’t always require literal self-replication; it can work whenever some configurations outlast or outperform others. As Hazen et al. put it, Darwin’s natural selection is just one instance of a “far more general natural process”. They note that some biologists object to using the term “evolution” for things like minerals or stars because of the lack of genetic inheritance. However, if we abstract away the specific mechanisms, the logic of selection applies broadly. Indeed, Hazen’s “law of increasing functional information” was explicitly intended to apply “to both living and nonliving evolving systems”.

One might ask: is there any system where selection wouldn’t eventually produce complexity if given variation and time? If the selection criterion is trivial (or if there’s no criterion at all), then complexity might not increase. For instance, if survival is purely random (no advantage to complexity), then you won’t see a trend – you’d just get drift. Or if the environment is static and favors one simple configuration strongly above all others, the system might evolve to that simple optimum and then stop (no further complexity needed). But in many interesting systems, especially open ones with changing environments or competitive interactions, there is pressure for continued adaptation, which can drive continued complexity.

Static vs. Dynamic Selection:

It’s worth distinguishing static environments (selection for one optimum state) versus dynamic or open-ended environments (where the targets or niches keep changing or expanding). Complexity is more likely to dramatically increase in the latter, because the goalpost moves or new niches appear, requiring additional FI to exploit. Earth’s biosphere has been dynamic – oxygen emergence, climate changes, species co-evolution – all these ensured no single simple configuration could dominate permanently; thus complexity kept ratcheting up in some lineages to meet new challenges or opportunities.

We can conclude that evolution by natural selection is not an anthropomorphic concept but a logical framework applicable to any system with certain properties. It serves as a universal engine of complexity, given it has something to act on. The universality of Darwinism strengthens our hypothesis that complexity increase is a general phenomenon: wherever such an engine operates, complexity measured as functional information will tend to rise.

Complexity as a Directional Arrow of Time

We now address directly the concept of complexity as an arrow of time – the idea that as time progresses, there is a discernible direction in which complexity grows (at least in certain parts of the universe), much like entropy’s inexorable increase provides a time arrow. Is complexity’s increase sufficiently general and persistent that we can treat it as an arrow of time? And if so, what does that imply about the nature of the universe?

Empirical Observations:

From the perspective of 13.8 billion years of cosmic history, one can narrate an “arrow” of increasing complexity:

• Immediately after the Big Bang, the universe was nearly homogeneous plasma.
• By a few hundred thousand years, it was mostly hydrogen and helium gas (atoms formed).
• By a few hundred million years, the first stars and galaxies (structured collections of particles) formed.
• Over billions of years, successive generations of stars created heavier elements, which formed planets and more chemically diverse environments.
• About 4.5 billion years ago, Earth formed; by ~4 billion years ago, chemical processes on Earth led to the first proto-life (simple self-replicating molecules).
• Life then increased in complexity through single-celled to multicellular (by ~600 million years ago complex animals appeared), then through the Cambrian explosion to even more complex forms.
• Intelligence and tool use evolved (our hominid ancestors in the last few million years), culminating in a technological civilization (present day) that introduces new forms of complex structures (cities, computer networks).

This storyline suggests a cumulative trend. Of course, it is biased in that we are focusing on one region (Earth) and one outcome (us) as emblematic. The universe as a whole is mostly still vast space with simpler structures like stars and diffuse gas. But the existence of even one trajectory from Big Bang to sentient life is telling: it shows what is possible under the laws of physics. And if it happened in one place, it might in others, making it part of the universal story rather than a fluke.

There is also a quantitative aspect to this arrow. Eric Chaisson’s plots of free energy rate density, mentioned earlier, show an upward trend when plotted against time of origin. For example, he estimates:

• Early stars: Φ (energy flow density) on the order of 1 erg/s/g.
• Modern sun-like stars: a few erg/s/g.
• Simple plants: tens to hundreds of erg/s/g (they process more energy per mass through metabolism).
• Animal bodies: hundreds to thousands.
• Human brain: ~10510^5 erg/s/g (very high energy throughput relative to its mass). He notes an apparent exponential increase over time, with humans at the top end currently. While energy rate density is just one measure, it correlates with organizational complexity (brains are more complex than stars). Thus, one could say the capacity to process energy/information has increased, marking a direction.

The Role of Entropy Production:

Why does complexity often increase? Non-equilibrium thermodynamics provides an answer: systems will evolve structures that dissipate free energy effectively. This is sometimes called the “MaxEnt Production” conjecture – that systems with many degrees of freedom often find pathways to maximize entropy production. This can drive complexity because complex organized systems can sometimes dissipate energy faster than simple ones. For instance, a forest (complex ecosystem) is very good at capturing sunlight and producing entropy (through respiration, decay, etc.) compared to bare rock. The biosphere increased Earth’s overall entropy production by exploiting sunlight more fully (e.g., formation of soil, etc., that wouldn’t happen on a lifeless planet). Thus, there is a synergistic link: the arrow of entropy (global increase) may channel a local arrow of complexity (complex structures form to aid in entropy production). This idea was championed by Schneider and Kay (1994) who argued that life is a response to energy gradients – basically, life is what happens as an efficient way to degrade the solar gradient.

Irreversibility of Complexity Build-up:

Complexity’s arrow, like entropy’s, has an aspect of irreversibility. Once information is generated, it tends to persist (barring large disturbances). For example, the genetic information in modern organisms traces all the way back – it doesn’t spontaneously revert to a simpler form. The biosphere will not spontaneously go back to just bacteria everywhere; that would require some cataclysm (which is an input of energy or change, not a spontaneous reversal of time). Similarly, the structures in the universe (galaxies, etc.) won’t just smear back into homogeneous gas without some dynamic cause. In this sense, complexity increase where it has occurred has a “memory” – it’s recorded in physical structures and cannot be easily undone. This memory is one reason complexity can keep building (it builds on prior complexity).

Exceptions and Non-Monotonicity:

It must be acknowledged that complexity’s arrow is not as uniform or omnipresent as entropy’s. Entropy increases inexorably in a closed system. Complexity can decrease under some circumstances – e.g., mass extinctions can wipe out complex organisms, leaving simpler survivors. After the End-Permian extinction (~252 million years ago), the number of very complex land vertebrates dropped dramatically; complexity in ecosystems took a hit. However, it recovered and then exceeded previous levels (the Mesozoic had even more varied large animals). So, complexity’s arrow might zigzag – periods of increase, occasional setbacks, but an overall trend upward over the very long term (at least on Earth). Complexity also doesn’t increase everywhere: some environments remain simple (e.g., the deep subsurface of Earth still has only microbial life, which is not much more complex than billions of years ago). The arrow appears when you look at the maximum or the frontier of complexity in the most innovation-rich systems.

It’s valid to ask: is this arrow of complexity an inherent feature of the laws of nature, or a contingent outcome? This is a deep question. If one rewound and replayed the universe, would complexity always emerge and increase? Simon Conway Morris argues convergently that intelligence and complex life might be almost inevitable given enough time, suggesting a built-in arrow. Gould argued it’s highly contingent (replay the “tape of life” and you’d get a different outcome, maybe not intelligence). Even if contingent, as long as the possibility space allows complexity, and there are selection mechanisms, complexity likely will emerge somewhere in the universe’s phase space – which is enough to call it a tendency.

Analogy with Entropy’s Arrow:

We can draw an analogy: Entropy increase is guaranteed by the second law, but it doesn’t guarantee where entropy is produced fastest or what intermediate states appear. Complexity increase is not “guaranteed” by a simple law in the same way, but it appears to be encouraged by the way physical laws permit local entropy reduction via energy flows. We might say complexity has a weak arrow – a general push in one direction – as opposed to a strict law. Part of the aim of this thesis is exploring if we can strengthen that to a law-like statement (with conditions) as Hazen’s team attempted.

In summary, complexity does function as an arrow of time in many contexts. The past was simpler; the present is more complex – at least in our corner of the universe. The key distinction: entropy’s arrow is universal and unavoidable, whereas complexity’s arrow is conditional (it manifests in regions where certain conditions – energy flow, variation, selection – are met). Nonetheless, given that those conditions appear naturally (stars, planets with flux, etc.), complexity’s arrow might be almost as cosmically pervasive as entropy’s, albeit in a patchwork fashion.

A Possible New Law of Thermodynamics? Physical and Philosophical Implications

Is there a new law of nature waiting to be articulated – one that codifies the growth of complexity analogous to how the Second Law codifies entropy growth? If so, what would it look like and what are its implications for physics and philosophy? In this section, we discuss the idea of formulating such a law and the conceptual shifts it might entail.

The “Law of Increasing Functional Information”:

We have already introduced the proposal by Hazen, Walker, et al.: “The functional information of a system will increase if many different configurations of the system undergo selection for one or more functions”. Let’s unpack this. It is structured similarly to the Second Law: the Second Law says “entropy of a closed system stays constant or increases.” The proposed law says “functional information of a (open, varying, selected) system stays constant or increases (and practically increases if selection is ongoing).” It’s not as succinct as “entropy increases,” but then, entropy’s law comes with qualifiers (isolated system). Here the qualifiers are important: you need (a) many configurations tried, and (b) selection for function. Those imply an open system with some mechanism of variation and some criterion – in other words, an evolving system.

One implication of articulating this as a law is to elevate the status of evolutionary processes to something fundamental in nature. It suggests that the emergence of complexity is not just a random fluke on Earth but a lawful process that would happen under suitable conditions anywhere. It is a unifying statement: it puts living and nonliving under one framework. It tells physicists that perhaps their list of laws is incomplete without something that addresses information and evolution.

Philosophically, this is significant because it challenges reductionism. Reductionism holds that all higher-level phenomena (like life, mind, etc.) are explained by known physical laws (quantum physics, etc.). In a reductionist’s perfect world, one wouldn’t need an additional law of complexity; the second law and initial conditions would suffice. However, if one finds that no combination of known laws and reasonable initial conditions can easily explain the emergence of complexity we see, one might suspect a missing principle. It might be akin to how in the 19th century, one could in principle explain a thermodynamic engine by Newton’s laws applied to molecules, but in practice a higher-level law (second law) was formulated to capture an emergent regularity (heat flows one way) without tracking all molecules. Similarly, a law of increasing FI would capture an emergent regularity of complex systems without solving the Schrödinger equation for zillions of particles.

Consistency with Second Law:

Any new law must, of course, not contradict established ones. Hazen’s proposal is explicitly stated to be consistent with the second law. Indeed, it works in concert: selection processes require energy flow (to generate variations, to build structures), which inevitably produce entropy. Our law doesn’t make entropy decrease; it just says in the process of increasing entropy, the system can self-organize to increase functional info. One thought experiment: imagine a universe identical to ours in physical laws except that it somehow lacked the mechanisms for selection (perhaps all processes are either completely random or always go to equilibrium quickly). That universe might still increase entropy but might never build much complexity. The fact our universe does build complexity indicates there is an additional principle at play – selection for function – which our proposed law encapsulates.

A “Fourth Law”?:

If we consider classical thermodynamics, we have four laws (including the zeroth). Some have playfully suggested a “fourth law of thermodynamics” that addresses self-organization. For instance, the Constructal Law (Adrian Bejan, 1997) says that flow systems evolve to maximize flow access (which often leads to branching structures, etc.). It’s an attempt at a general law of design in nature. The law of increasing FI could similarly be seen as a “fourth law” – but it is broader than thermodynamics since it involves information and selection.

One philosophical implication is that information might need to be recognized as a fundamental quantity in physics, akin to energy or entropy. In recent decades, physicists have indeed increasingly viewed information as fundamental (e.g., black hole information paradox, Landauer’s principle relating information erasure to entropy). If a law of increasing FI holds, it means that information (of a certain kind) naturally accumulates in the universe. That might have deep connections to how we understand time and causality. For example, the universe could be seen not just as running toward heat death, but also running toward higher complexity pockets – two arrows intertwined.

Teleology without Teleology:

A new law of complexity might make the universe appear teleological (purpose-driven toward complexity), but it really isn’t teleology in the mystical sense – it’s a natural law, a blind process. However, such a law would formally articulate a kind of direction or “trend” that one could mistake for purpose. Philosophers of science would likely debate whether this imbues the cosmos with a direction akin to purpose or is simply a neutral tendency.

Testability and Falsifiability:

For a law to be scientific, we need ways to test it. How could we test a law of increasing FI? One way is through computer simulations and experiments:

• In artificial life simulations, does functional info reliably increase? (Generally yes, if selection is present, it should.)
• In observing different systems (e.g., comparing planets or environments), do we see that those with more opportunities for selection have higher complexity? For example, Earth vs. Mars – Earth has life, Mars seemingly not; Earth had more dynamic conditions perhaps, or just luck. If we found life on Mars in the past, it would support that wherever possible, complexity arises.
• One could potentially use chemical networks in the lab: set up two scenarios, one where selection is operating (say a recursive selection process like a serial transfer experiment for autocatalysis) and one control where it’s just random, and measure if FI (for some defined function) goes up in one and not the other.

If the law is true, it suggests that whenever we find a system that has undergone many selection iterations, it should have more FI than it started with. If we found contrary evidence (e.g., a long-lived ecosystem that somehow lost complexity without any external disturbance), that would challenge it. So far, life’s history doesn’t give such contrary evidence at the macro scale – complexity has generally risen, though not monotonically.

Philosophical Shift – from Being to Becoming:

Traditional physics is mostly about being – states of systems and timeless laws. An evolutionary law is about becoming – it’s inherently time-oriented and creative. Accepting a law of increasing complexity would be a shift towards seeing the process of the universe as something that can be lawfully characterized, not just the outcomes. It aligns with a process philosophy view (like those of Alfred North Whitehead or Teilhard de Chardin’s ideas, albeit now in scientific garb).

It’s noteworthy that the law of increasing FI is not deterministic in detail; it doesn’t tell you which complexity will arise, just that some will under selection. This introduces a law with an element of probability and contingency, similar to how the second law is statistical (entropy likely increases, though fluctuations can decrease it locally). This might herald a new kind of law in physics that is less rigidly predictive of exact events and more about overarching trends. Some philosophers might argue whether that qualifies as a “law” in the strict sense, but in practice the second law itself is statistical.

Relation to Information Theory and Computation:

Another implication is connecting to computation. The universe producing increasing FI could be seen as the universe performing computation – natural processes computing solutions to constraints (like evolution “computing” an eye design). Some like Seth Lloyd have even said “the universe is a quantum computer” that has been computing its state all along. If complexity growth is lawlike, then maybe the universe inherently computes increasingly complex structures. There’s an analogy to be made with algorithmic information: the output of certain computations increases in algorithmic complexity over time. Perhaps the universe’s time evolution is akin to running an algorithm that generates complexity (except, of course, it’s not aiming for complexity, it’s a side effect of running physics with certain boundary conditions).

Limits of the Law – The Entropic Doom:

One sobering consideration: if the law holds now, will it always? Eventually, as the universe approaches heat death (if indeed it does), free energy sources will wane. Complexity can’t increase without energy flows. So in a cosmological sense, complexity’s arrow might only run during the universe’s middle age, not at the end. In endless expanding universe scenarios, stars burn out, and unless new energy sources (like proton decay or something exotic) feed complexity, it might plateau or decline. So the law might be epoch-dependent. However, that doesn’t invalidate it as a law applying whenever conditions are right, much like life can’t persist without energy but given energy, life emerges.

In conclusion, positing a new law akin to a thermodynamic law for complexity is both exciting and challenging. It forces us to broaden our conception of fundamental principles to include those that talk about evolution and information, not just static quantities. If embraced, it could unify disparate fields under a common principle and guide the search for complexity elsewhere (as we’ll see in astrobiology implications). It also elevates the status of function in scientific discourse – moving it from a concept mostly used in biology into fundamental physics (something even a rock has in context). This bridging of teleonomic language (function, selection) with physics might be one of the biggest philosophical shifts from this line of thought.

Evolving Function and Context: What Counts as “Complex”?

One of the subtler aspects of our hypothesis is that what we consider “complex” is not absolute – it evolves as functions and contexts evolve. In other words, complexity is, to a degree, in the eye of the beholder (or in the “needs” of the system): it depends on what function you care about and the context in which a system operates. As systems become more complex, they also redefine the criteria for complexity at the next level. This recursive aspect is crucial for understanding open-ended evolution.

Context-Dependence of Functional Information:

As described earlier, functional information is defined only with respect to a chosen function. For a single enzyme, FI could be measured for the function “catalyze reaction X”. But that enzyme might also incidentally catalyze a very slow version of reaction Y or bind some other molecule weakly – if we considered those as the function, the FI would be different. Typically, in evolution, the function is dictated by what the environment “rewards.” For early life, a “function” might be simply self-maintenance in a chemical sense. Once life had cells, new functions became relevant: motility, capturing light, etc. The complexity measured relative to those functions then began to increase.

For example, the complexity of a bacterium can be measured by how much information it encodes to survive in its niche (nutrient metabolism pathways, etc.). Now consider a multicellular organism, say a sea sponge. In one sense, a sponge is more complex than a bacterium – it has multiple cell types and a larger genome. But if we asked, “how complex is a sponge’s genome relative to performing basic metabolism?” it might have a lot of extra DNA that isn’t needed for metabolism but is needed for multicellularity. In the context of “metabolism,” the sponge is over-specified; in the context of “forming a multicellular body with some cell differentiation,” the bacterium has essentially zero capability, whereas the sponge has the necessary information.

Thus, new context enables new functions which then define new measures of complexity. When life became multicellular, “organismal complexity” became a thing – and we start counting cell types or tissue specialization as complexity. When brains evolved, “neural complexity” or cognitive function became a new context – a simple brain might be considered functionally simpler in that context than a complex brain, whereas in the context of survival both suffice for their organisms.

In technology, a similar phenomenon: The complexity of a mechanical calculator from the 1950s is high relative to the function “do arithmetic faster than a human.” But in today’s context, that’s trivial – a basic phone chip does that easily; now complexity is judged by functions like “run a global communication network.” So as capability grows, what we label as complex often shifts upward. This can make it tricky to have a single metric over long time spans, but functional information handles this by always tying to a specified function. It means we have to update our perspective as new functions appear.

Exaptation and Change of Function:

In evolution, exaptation is when a trait evolved for one function gets co-opted for another. For instance, feathers might have initially been for insulation or display, later co-opted for flight. When the function changes, what is the complexity? Feathers had some FI for insulation originally; later they had FI for flight. The context changed (the organism started gliding, etc.), and now the measure of complexity of the feather structure would be made with respect to aerodynamic properties, which is a new metric. The feather then might become more refined (increasing FI for flight).

This tells us that complexity is not just accumulating in one dimension; it branches into new dimensions. Life’s complexity did not all focus on one task getting harder and harder; instead, new tasks/goals emerged. Initially “metabolize and replicate” was the task, later tasks like “move fast,” “sense environment,” “think” emerged, each adding new layers of complexity. It’s as if evolution itself creates new axes of complexity. This is important: the space of possible functions expands as complexity grows. Early life had no “sight” function – there was nothing to see perhaps. Once light receptors evolved, “see better” became a possible axis along which complexity could further increase (e.g., evolving eyes).

So complexity begets complexity: a modest increase in complexity (like a light-sensitive spot) created a context (organisms respond to light) where improving that (making an eye) became a new frontier for FI increase. Kauffman’s adjacent possible fits here – each new feature opens a door to further features.

Measuring Complexity at Different Levels:

We often ask “which is more complex, a human or a bacterium?” Most would say a human. But objectively, a bacterium might have a more complex chemistry in some ways (certain bacteria have many metabolic pathways humans lack). How do we compare? It depends on what features we compare and in which context. Generally, because humans have not only complex bodies but also brains and societies, on any holistic measure (number of distinct cell types, amount of non-redundant DNA, number of behaviors), humans outrank bacteria. However, put a human in the context of surviving in a deep-sea hydrothermal vent – the human is non-functional, the bacterium thrives. Complexity isn’t just about being complicated; it’s about being fit to context.

Thus, adaptation to context is a form of complexity – often called organized complexity. A system that is complex but not adapted (like a random tangle of computer code) is arguably less interesting than one that is equally complex but does something useful. In evolution, useless complexity is pruned away typically (it carries a cost). So evolved complexity tends to be relevant complexity.

Functional Complexity vs. Random Complexity:

This evolving nature of function addresses a confusion: entropy increase can be seen as “random complexity” (shuffled mess) increasing, which is not what we refer to. Organized complexity is different. As context changes, the organization shifts but still remains non-random. We might think of effective complexity (Gell-Mann’s term) which is roughly the length of a description of the pattern (excluding randomness). That effective complexity tends to increase in evolved systems because more structured patterns accumulate. But if a system became largely random, we wouldn’t count that as high complexity in the meaningful sense (though algorithmically it’s high). Evolution avoids pure randomness except at the mutation level; selection filters it into design.

How Context Evolves:

Context is often shaped by previous complexities. For life, the environment of evolution is partly the physical environment and partly other organisms. As life got more complex, the biotic environment (predators, competition, symbiosis) became a key context driving further complexity (Red Queen hypothesis – an arms race of complexity between predators and prey). Similarly, once humans started creating culture, the context for human evolution (and especially cultural evolution) became largely cultural itself – we now evolve in response to problems we ourselves created (like needing education to function in society, etc.). So context itself can become complex, leading to a feedback loop: complexity in organisms -> complex environment (including ecological webs) -> pushes more complexity in organisms.

In the nonliving domain, context can evolve too. A star’s context might be the galaxy’s chemical makeup. Early stars had only hydrogen/helium, later stars formed in contexts enriched by heavy elements (which allow planets, etc.). So the context for star/planet formation changed over cosmic time, leading to planets with more ingredients (complex minerals, etc.). That in turn allowed life (context for chemistry changed by presence of certain minerals maybe).

Implications for Measurement:

If context and function evolve, any static measure of complexity might fail to capture progress. We might need a multi-faceted measure that tracks complexity on various fronts. For instance, “genomic complexity,” “neuronal complexity,” “social complexity” are all different. One could imagine a vector of complexity metrics. But the law of increasing FI suggests an overall increase in the sum total FI (across all relevant functions). For a biosphere, one could sum FI over all functions that organisms perform. That sum definitely went up over time, as new organisms filled new functional niches. It’s tricky to compute, but conceptually, early life had maybe a dozen metabolic functions; today, life collectively has thousands of distinct ones (from nitrogen fixation to vision to language capacity in humans). Each of those had an FI cost to evolve.

In summary, complexity is a moving target. The evolutionary process redefines complexity as it goes by generating new contexts and criteria. Our hypothesis embraces this: the increase in complexity is not just in one dimension, but in an expanding dimensional space of possible functionalities. This is a hallmark of open-ended evolution – the system is not approaching a fixed maximum complexity; instead, it keeps inventing new forms of complexity. Any prospective “law of complexity” must account for this evolving target: rather than “maximize X,” it’s “introduce new X, Y, Z and increase them,” an ever-changing objective. This again ties to the Gödelian idea – you can’t have a final theory of complexity because the system can always add a new layer that wasn’t in your model’s vocabulary.

Appreciating the evolving nature of function also cautions us in detecting complexity elsewhere: if aliens have completely different biology, what is complex to them might not be obvious to us because of different context. We need general measures like FI to detect it on their terms.

Sudden Jumps and Phase Transitions in Complexity

The evolutionary record of complexity is not a smooth, gradual incline but is punctuated by sudden jumps – moments in history where complexity leapt to a new level relatively rapidly (in geological or cosmological terms). These can be seen as phase transitions in the organization of matter and information. Understanding these transitions is key to our hypothesis, because it is often at these junctures that entirely new forms of selection and complexity arise.

Figure: A schematic timeline of major evolutionary transitions in information processing, from abiogenesis (green, biochemical complexity) through biological evolution (yellow, multicellular life and brains) to cultural/technological evolution (orange/blue). Each arrow represents a phase transition where a new level of complexity emerges (RNA to DNA/protein world, single cells to multicellular organisms, brains enabling abstract information, and digital technology). Such transitions create new contexts (genotype-phenotype relationships, social behavior, etc.) that open additional complexity pathways (based on Gillings et al. 2016).

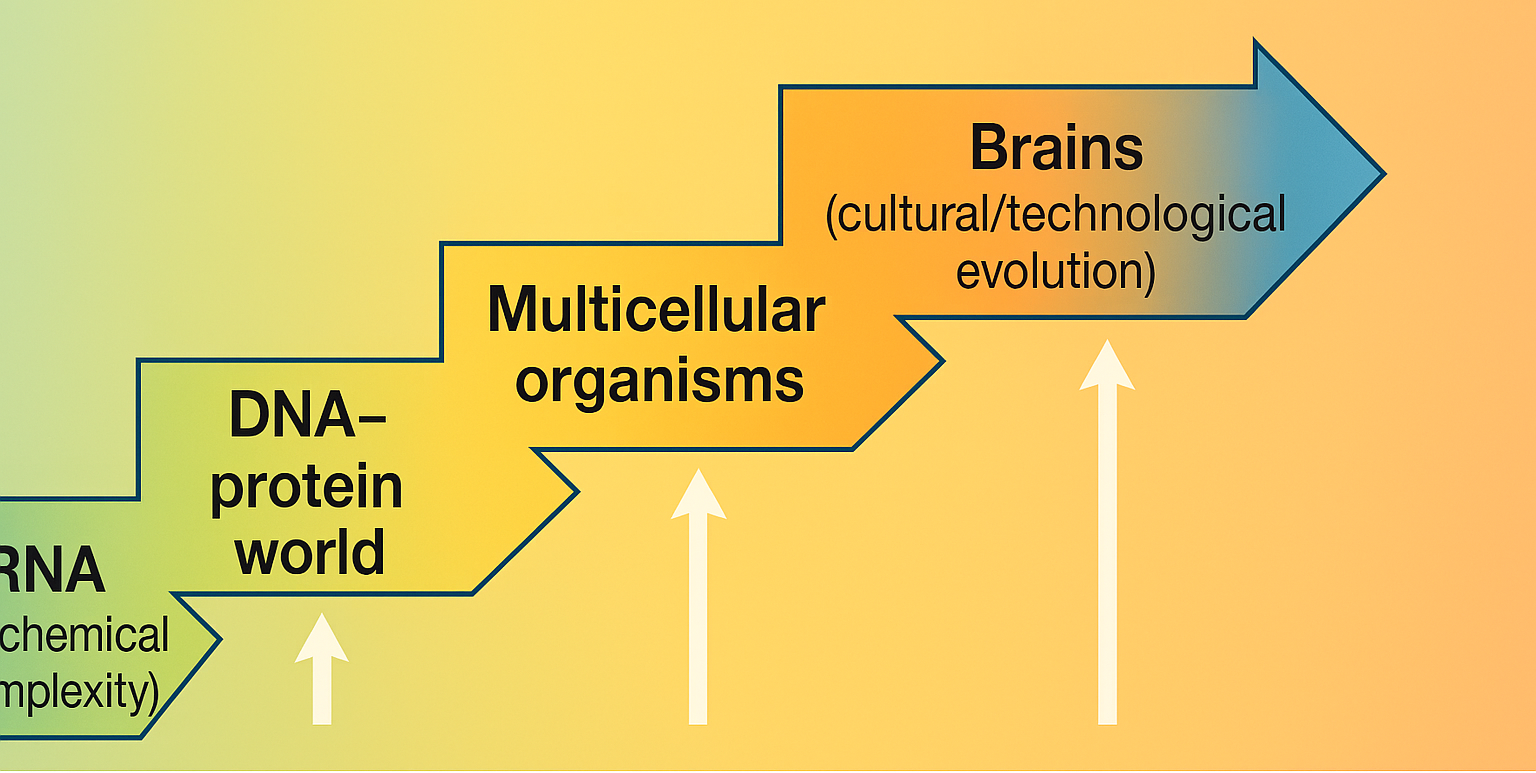
Origin of life (abiogenesis):

Chemistry to biology. This is arguably the biggest leap – going from no self-sustaining information-bearing system to the first genetic system. Before this, there was no Darwinian evolution; after, there was. In complexity terms, it might be compared to a phase transition: once a critical threshold of molecular complexity and network integration was crossed, a self-replicating system became autocatalytic and took off, much like cooling water suddenly crystallizes at a certain point. Various hypotheses (RNA world, metabolism-first, etc.) try to explain how this jump occurred. It might have been a gradual lead-up with a tipping point where true replication emerged. But from a high-level view, the state of Earth “flipped” from non-living to living around 4 billion years ago, introducing an entirely new regime of complexity growth.

Origin of the genetic code (RNA to DNA/protein world):

Life started perhaps with RNA doing both tasks of information and catalysis. The development of a dedicated information storage (DNA) and dedicated catalysts (proteins) was a transition that allowed genomes to expand (DNA is more stable) and catalytic diversity to increase (20 amino acids vs 4 RNA bases). This may have been relatively quick once the mechanism (like reverse transcriptase or something) was in place.

Origin of eukaryotes (complex cells):

The jump from prokaryotic (simple) cells to eukaryotic (complex, with nucleus and organelles) was huge. It involved endosymbiosis – one cell living inside another to become mitochondria (and chloroplasts in plants). This is like a merger of organisms to create a higher complexity cell, with internal division of labor. Fossil evidence suggests that for over a billion years after life’s origin, cells remained prokaryotic; then roughly 1.5-2 billion years ago eukaryotes appeared, and soon after, many new capabilities (multicellularity, larger genomes) followed. This looks like a phase change unlocked by symbiosis: before, cells were limited in size/energy; after, a eukaryote could be 1,000 times larger and have energy-rich mitochondria to support larger genomes.

Origin of multicellularity:

This happened multiple times independently (plants, animals, fungi, algae each did it). It is a transition where individual cells (which could live alone) stuck together and specialized. There is usually a relatively quick initial jump – a group of cells becomes an integrated unit (possibly via staying together after division, or clumping). This opens the door to huge complexity increases: cell differentiation means the organism can have tissues, organs, etc. The Cambrian explosion (~540 million years ago) might be seen as a secondary phase transition following multicellularity: once the genetic mechanisms for patterning a body (e.g., Hox genes) were in place, an explosion of new body plans occurred relatively rapidly.

Origin of societies (eusociality) and language:

In animals like insects and then humans, individuals formed larger cooperative groups (ant colonies, human tribes/civilizations). Human language is a big one – suddenly information could be exchanged and accumulated culturally rather than genetically. We got an evolutionary transition from biological evolution to cultural evolution. Human society’s complexity (cities, etc.) is qualitatively beyond what solitary humans or small kin groups could achieve. Anthropologists see the relatively rapid emergence of agriculture and then civilization as a phase transition on Earth – in a few thousand years (very short on evolutionary time), complexity of societal organization skyrocketed.

Each of these transitions has the character of a phase transition: the system reaches a critical threshold where a new order parameter (new organizing principle) emerges. Like water turning to ice – once below 0°C, a new crystal lattice forms spontaneously. For life, the “control parameters” could be things like environmental conditions or pre-existing complexity reaching a point where synergy can happen (like enough different molecular species for an autocatalytic set to form, or enough mutual benefit for cells to stick together, etc.).

Nonlinear Dynamics:

Complexity jumps often involve positive feedback. For example, once a primitive replicator exists, natural selection kicks in, which rapidly (exponentially) increases its frequency and drives improvement – a feedback loop. Endosymbiosis: once a host cell and symbiont cooperate, their combination can outcompete others, spreading this innovation quickly. These feedbacks mean that transitions can be fast relative to background evolution.

Loss and Gain:

After a jump, sometimes complexity can simplify in parts. For instance, an integrated multicellular organism might simplify some components (cells lose independence, some genes lost if redundant). But overall, a higher level of complexity is established. This is like when a liquid becomes solid – locally some freedom (fluidity) is lost, but global order increases. Similarly, cells in a body lose some autonomy, but the body-level complexity is a new emergent structure.

Universality of Transitions:

Phase transitions in physics have universal properties (e.g., critical exponents, etc.). Is there anything universal about complexity transitions? One idea: criticality at “the edge of chaos.” Some complexity theorists (e.g., Chris Langton) speculated that life operates at a poised state between too much order and too much chaos – at a phase transition between solid-like and gas-like behavior, metaphorically. That might be where computation is best, etc. It’s an open question if life inherently self-organizes to such critical states. Possibly, each major transition finds a new “edge”: eukaryotic cells balanced internal cooperation vs competition of components, multicellularity balanced cell growth vs cancer risk, etc.

Irreversibility of Transitions:

Once a new level emerges, it tends to persist. Eukaryotes never reverted to purely prokaryotes (though some symbionts simplify, they remain part of eukaryote lineage). Multicellular lineages rarely, if ever, revert fully to unicellular free-living forms – though some parasites simplify, they usually still require a host (which is a multicellular context). This irreversibility is akin to how after water freezes, you need to add energy (heat) to melt it; similarly, to break multicellularity, something drastic must happen (like an extinction that eliminates all multicell life – that didn’t happen after it arose).

Predictability and Contingency:

Phase transitions can sometimes be predicted if parameters are tuned. Were major transitions inevitable or chance? Some argue that certain transitions (like eukaryotes, intelligence) might be rare (contingent on unlikely events like the exact symbiosis event, or asteroid wiping out dinos to give mammals a chance). Others argue they might happen given enough time (maybe if not one symbiosis event, another would eventually do similarly). If our hypothesis is to argue a universal trend, we lean towards thinking these transitions, or analogous ones, would eventually happen under broad circumstances – they are attractors in the evolutionary dynamic landscape.

For instance, if life exists elsewhere, we might predict it too will go through transitions: perhaps not exactly the same (maybe no DNA, but some switch from a simpler genetic system to a more efficient one; maybe multicellularity analogs if life is multicellular-scale). The specifics can vary, but the pattern of hierarchical emergence might be general.

Non-biological Jumps:

Are there sudden complexity jumps in non-life? Possibly:

• Structure formation in the early universe can be seen as a series of transitions: particle physics phase transitions gave rise to structure (e.g., inflation ending, matter domination, recombination enabling atoms, etc.). Gravity causing first stars could be considered a transition from diffuse to star state in regions.
• Another example: the formation of the first black holes or first galaxies introduced new phenomena (e.g., galaxies have dynamics not present in just star clusters).
• Chemistry: perhaps when a reaction network becomes autocatalytic, that’s a transition akin to life’s origin.
• Some hypothesize a coming transition with AI or the merger of biological and digital (the figure hints at a “bio-digital fusion” as a future phase transition). That is speculation, but on Earth, the emergence of digital information processing (computers, internet) is indeed a radical new complexity regime in just the last century – arguably a phase change we are currently within.

In the scope of this thesis, understanding these jumps reinforces that complexity growth is not linear but occurs in spurts when conditions allow a new higher-order integration. The hypothesis of a general complexification trend must accommodate these leaps. In fact, one might say the trend is a stepwise function: long plateaus of incremental change, then a jump, etc. The jumps themselves could be seen as critical phenomena one can study – perhaps there are telltale signs approaching a transition (e.g., increasing variance, as in physics critical points). Some origin-of-life researchers look for signs of a system “on the brink” of life. Likewise, artificial life researchers try to create conditions for open-ended evolution (which might spontaneously produce new transitions).

To conclude this section: complexity’s increase often comes in the form of these major transitions. Each transition creates a new level of selection (e.g., selection at group level in multicell life, or at idea level in cultural evolution). These new levels then continue the process of complexity increase, possibly leading to subsequent transitions. Recognizing and studying these transitions helps us understand the mechanisms that drive big leaps and how likely they are, which in turn informs our expectations for complexity elsewhere (like, will life inevitably get complex or might it stall before a transition?).

Self-Referential Systems and Gödelian Incompleteness: Epistemological Implications

Complex systems that evolve and can incorporate representations of themselves or their environment raise deep epistemological questions. In particular, when a system becomes sufficiently complex to be self-referential (able to contain information about itself, reason about itself, or produce new forms beyond what’s pre-specified), we encounter limits analogous to Gödel’s incompleteness in formal logical systems. This section explores these analogies and their implications: can an evolving system ever be fully understood from within? Are there inherent unpredictabilities and “unknowables” in open-ended evolution?

Self-Reference in Biological Systems:

A hallmark of advanced life (like humans) is the ability to create models of the world that include the self. Our brains have self-models; we contemplate our own thinking (metacognition). Even at a simpler level, any system with feedback has a form of self-reference (the system’s state affects its future state). When evolution produced brains that could predict and plan, life gained a form of self-reference: organisms not only adapted blindly but could anticipate outcomes and adapt behavior – essentially running internal simulations. This certainly complicates the evolutionary dynamic because now selection isn’t the only driver; intelligence can direct adaptation (for example, humans can decide to save endangered species or alter our environment consciously). The system (biosphere + humanity) is now aware to some extent of the evolutionary process itself.

In a computational analogy, once a program can modify itself or write new programs (self-replication in code or AI designing AI), you have a self-referential evolving system. There are known theoretical limits: e.g., the halting problem shows no system can perfectly predict all aspects of an equally powerful system (no program can generally tell if another arbitrary program halts). This is analogous to how no sufficiently complex organism can foresee all consequences of any possible mutation – the space is too vast and essentially uncomputable in full generality.

Gödel’s Incompleteness Theorem Analogy:

Gödel showed that any consistent formal axiomatic system that is rich enough (to include arithmetic) cannot prove all true statements about the natural numbers – there are true statements it can’t prove (and it can’t prove its own consistency). How is this relevant to evolving systems? We can draw analogies:

• Think of the “theory” or set of rules that describes an evolving system’s behavior as akin to an axiomatic system. If the system can effectively represent that theory within itself (self-modeling), perhaps there are truths about its future behavior it cannot derive internally.
• An evolving system can produce novelty that was not derivable from its initial state description without simulating the evolution. In a sense, the only way to know what evolution will invent is to actually run evolution – there’s no shortcut algorithm to deduce all future adaptations (this is related to undecidability).
• Kauffman and colleagues explicitly argued that “no laws entail the evolution of the biosphere”. They mean that one cannot pre-specify a set of exhaustive laws that would let you derive all future evolutionary adaptations, because evolution keeps generating new functions and niches, which reframe the “laws.” This is analogous to how adding a Gödel sentence (a new true but unprovable statement) effectively requires going to a stronger system – evolution similarly might require extending your model to capture new functionalities post hoc.

So, the epistemological implication is that there may not be a finite, closed-form theory of evolving complexity that is both complete and consistent. We might always be surprised by novel forms. This doesn’t mean we can’t have useful laws (like the law of increasing FI) but it means any such law will be general and not fully predictive of specifics.

Unpredictability and Creativity:

Evolutionary processes are famously hard to predict in detail. Weather provides a simpler analogy – chaotic systems can’t be predicted long-term because small uncertainties blow up. Evolution adds to chaos the combinatorial explosion of novelty. It’s not just sensitive to initial conditions; it creates new conditions. In creative systems (like technology innovation, or cultural evolution of ideas), people often use terms like “no one could have predicted invention X at time Y” except in hindsight. Similarly, the emergence of, say, the first bird or the first human intelligence could not be forecast by a “universal biology equation” – none exists that could tell that at year N some species will be discussing physics.

This unpredictable creativity is a strength of the hypothesis: if complexity always increased in a simple predictable path, it might hit a ceiling or at least we could pre-compute it. The fact it doesn’t suggests it can keep unfolding new surprises (which is exactly why complexity can keep rising without bound in principle).

Limits of Knowledge for Inside Observers:

Consider that we (humans) are part of the evolving system, trying to understand it. Gödelian analogy might imply we can’t fully understand a system that we’re a part of with a model that is simpler than the system itself. We can approximate and learn patterns (like we learned about natural selection and even articulated a law of increasing FI), but we might not be able to foresee, for example, the next major transition or the eventual implications of our own technological evolution.

In a more abstract sense, a self-referential system can ask questions about itself that it can’t answer without essentially changing itself. For instance, the human brain trying to understand consciousness might be inherently limited – can a conscious system fully comprehend its own emergence? Some argue no, citing a Gödel-Turing type limitation (this is speculative but debated in philosophy of mind).

Open-Endedness and Incompleteness:

In artificial life research, open-ended evolution is a goal: they want simulations where complexity keeps increasing with novelty, not plateauing. It’s proven very challenging – many simulations stagnate after a while. One thought is that the simulations are done in a defined, closed environment with fixed rules; perhaps truly open-ended evolution requires that new rules/contexts can emerge (which is hard to implement in a computer program without just explicitly allowing random rule changes). This itself reflects the incompleteness idea: any system with fixed rules might not generate endless novelty; you may need a way for rules to evolve, which leads to a system that can’t be fully analyzed by the initial rule-set alone.

So perhaps life’s secret is that it constantly breaks the symmetry or uniformity of rules by creating new higher-level “rules” (e.g., chemical rules gave way to biological natural selection rules, which gave way to cultural norms, etc.). Each step goes beyond a fixed formal structure.

The Role of Self-Reference in Consciousness:

Some have drawn parallels between Gödel’s theorem and consciousness or free will (e.g., Penrose’s arguments, though contested). Without going deep into that, one can say a conscious brain is a self-referential system (it forms “I” concept). If indeed such a system can’t be perfectly predicted by any external observer without essentially simulating it at full scale, it means there’s an epistemic barrier – you can’t compress the complexity of a self-aware evolving system into a simpler predictive theory.

Implications for a Theory of Complexity:

If a law of increasing complexity exists, it might be more like a meta-law – it tells us that complexity increases and maybe conditions when, but it might not be able to tell specifically what forms that complexity will take beyond statistical properties. This is similar to how the second law tells us entropy increases but doesn’t give the exact microstate trajectory – it’s a statistical law. We might have to content ourselves with similarly statistical or high-level predictive power for complexity, not precise control.

For scientists and philosophers, this positions evolution and complex systems in a realm where complete reductionist prediction is impossible, thus valuing approaches that emphasize understanding processes and capabilities rather than exact outcomes. It also fosters humility: we might not ever have a “Theory of Everything” that includes the open-ended creativity of the universe’s complex systems. Instead, we might have to accept an endlessly unfolding frontier of knowledge as complexity grows.

Practical Upshot:

Understanding these limits does not prevent us from using the complexity trend. For example, in astrobiology, we can predict if life starts on a planet, it may eventually produce tech signals without knowing exactly what aliens will build – we just guess they’ll exploit increasing complexity and energy use, hence might emit detectable signals (like radio). That’s a probabilistic prediction using the idea of complexity increase, albeit acknowledging we can’t script alien history.

In summary, self-referential complexity and the analogy to Gödel’s incompleteness highlight that evolving systems have a kind of creative freedom that resists full encapsulation in initial axioms. This insight underscores the uniqueness of evolutionary processes compared to simpler physical processes and is a philosophical justification for treating complexity growth as something novel (maybe deserving of a “law” as we propose). It also means our understanding of the universe’s complexity will always be, to some extent, open-ended – there will always be new phenomena requiring new understanding, as no final closed description can capture an open universe that includes its own observers and constructors.

Expanding Possibility Spaces and Emergent New Rules

A recurring theme has been that as complexity increases, the space of possibilities expands – new configurations, behaviors, and even new laws (or effective rules) emerge that were not accessible or relevant before. This section delves into how complexity opens up new possibility spaces and how, at higher levels of complexity, qualitatively new principles govern system behavior (often requiring new scientific descriptions). Essentially, we explore the idea that “new rules emerge from old ones” when a system crosses certain complexity thresholds, and how this contributes to the unending increase of complexity.

Emergence of Possibility Space:

Stuart Kauffman’s concept of the adjacent possible is illustrative: at any point, the system has certain components, and combining or varying them yields new combinations that were not present before – those are in the adjacent possible. Once realized, each of those opens further combinations. For example, once a cell evolved the ability to produce a certain enzyme, that enzyme’s presence could enable a new metabolic pathway, which opens the possibility of using a novel nutrient, which can lead to evolving in new niches, and so on. The “phase space” of biological systems isn’t static; it grows as life invents new genes and proteins. This is partly because life constructs its own environment (niche construction) – e.g., oxygenation of atmosphere by cyanobacteria created a whole new set of chemical possibilities.

Sara Walker and colleagues, in developing Assembly Theory, echo this: they define objects by their assembly pathways. Simple objects (e.g., a single molecule type) have few assembly steps; complex objects (a cell, or an artifact) require many steps (hence high assembly index). As more steps become possible, the space of objects explodes combinatorially. Crucially, selection prunes which ones actually appear, but over time, more complex objects accumulate. In assembly theory, they measure how selection is required to produce a given object abundance. If something needs a lot of selection (many assembly steps improbable without selection), it likely didn’t occur early but can occur late after intermediate steps are in place. So the timeline of the universe can be seen as gradually building up the “assembly” possible: first simple atoms (one step from fundamental particles), then molecules (few steps), then biomolecules (many steps, required selection to accumulate), then cells (even more steps). Each stage increased the maximum assembly index seen in nature.

Emergent Rules at New Levels:

We already discussed “More is Different.” Let’s give concrete cases:

Chemistry from Physics:

When you have many atoms bonding, you get emergent laws of chemistry. A lone electron and proton can be described by physics equations; a mole of interacting atoms gives rise to emergent concepts like temperature, pressure, acidity – which are not meaningful at single-particle level. These aren’t “new fundamental laws” but new effective laws (e.g., gas laws). Complexity here (number of particles) yields new regularities.

Biology from Chemistry:

Once replicating cells exist, we have the laws of genetics (Mendel’s laws, etc.), evolution by natural selection (a statistical law at population level), etc. These principles can’t be directly derived trivially from chemistry (you can in principle, but the emergence simplifies it: we don’t simulate every atom to understand natural selection).

Psychology from Biology:

A brain with billions of neurons has emergent patterns (thought, emotions) that neurobiology alone doesn’t fully capture; hence fields like psychology or cognitive science have their own principles, albeit grounded in biology. Society emerges from individuals, needing economics, sociology principles (like supply and demand or group behaviors) beyond individual psychology.

These emergent layers demonstrate that complexity produces novel effective rules of behavior. For example, in economics, an “invisible hand” emergent effect of markets might be observed, which doesn’t apply at the level of a single barter – scale and network complexity bring it out.

Downward Causation:

Sometimes people talk about higher levels feeding back to constrain lower-level dynamics (e.g., your mind’s decision (high-level) making neurons fire in a certain pattern (low-level)). This “downward causation” concept is debated, but in any case, the levels interact. New rules at a higher level can shape what configurations are stable at lower levels (like how societal norms influence which genetic traits prosper via cultural selection).

Why New Possibilities Mean More Complexity:

If complexity just kept refining within the same rules, you might hit diminishing returns (like just improving eye resolution has limits). But because new arenas appear (like evolving brains introduced culture, which introduced technology, which introduced digital life), complexity finds new directions to expand in. It’s like a tree that keeps branching. So complexity doesn’t just go up quantitatively; it diversifies qualitatively. That’s why talking about a one-dimensional “complexity” sometimes fails – it’s multi-dimensional.

Think of a game: at first level, you have a limited move set. You advance to level 2, new moves are unlocked. Evolutionary transitions are like unlocking new levels of a game with additional mechanics.

Universe’s Expanding Complexity Horizon:

Initially, the universe’s complexity was limited by physics of particles, then by simple chemistry, etc. As each threshold is crossed, the “ceiling” rises. There might still be absolute ceilings (maybe physics sets an upper bound on what complexity could exist given finite resources), but we haven’t hit that yet. Some theoretical work tries to estimate maximum possible complexity given physical constants – for instance, what’s the most computationally powerful system you could build with a given mass and energy (like Dyson’s eternal intelligence idea)? Those are speculative. But so far, every time one imagines a limit, something new bypasses it (like thought you can’t get more efficient than certain biology, then humans invented machines that surpass muscle power, etc.).

Rule Emergence and Scientific Paradigms:

From a philosophy of science view, as complexity gives new “laws,” science itself had to evolve by introducing new fields. There’s a historical correlation: only once phenomena emerged (like gas behavior, or evolutionary patterns) did we formulate laws for them. If truly new kinds of complexity arise in the future (say artificial superintelligence, or galaxy-spanning life, etc.), we might need entirely new scientific frameworks to describe those systemic behaviors.

Possibility Space in Technology:

We see expanding possibilities clearly in technology. Once you had computers, the space of possible software is enormous. Now with AI, the space of possible behaviors grows further (AIs designing stuff humans couldn’t). The internet interconnected human minds – creating new cultural genres (memes spread in ways that were impossible in analog era). Each innovation multiplies what can come next. There’s a concept of combinatorial innovation: every new tool can combine with existing ones to yield more than linear growth of possibilities.

Constraints and Selection Still Apply:

Importantly, not everything possible happens – selection and constraints funnel the trajectory. The presence of an expanding possibility space does not mean a random walk through it; certain paths are taken because of selection pressures or physical limits. But over long times, a lot of that space can be explored given persistent selection and variation.

Universe as Open-Ended Creative System:

If we step back, the picture emerges of a universe that, through complexification, is exploring an ever-growing space of states. Some states become stable or recurrent (like life, intelligence) – these might appear almost “inevitable” in retrospect because they are attractors in possibility space. Others are fleeting. If one were to re-run cosmic evolution many times, the specifics differ but one suspects certain broad “high-level outcomes” (maybe something like life or intelligence) would often appear because they are accessible attractors in an expanding possibility space under selection (this is debated but it’s a plausible view from complexity studies).

In essence, complexity’s increase is tied to the fact that with each step of increased complexity, the universe gains new ways to increase complexity further. This compounding capability may be why complexity has accelerated (life took ~4 billion years to get human-level intelligence, but human culture took mere thousands to get to moon landings, and possibly AI may surpass that in centuries – an apparent acceleration). Some call this acceleration the “law of accelerating returns” (Kurzweil) or similar – which is a specific observation that more complex systems evolve faster than simpler ones due to richer feedback and exploration of possibilities. This is yet another emergent pattern.

To summarize: The expansion of possibility space and emergence of new rules ensure that complexity’s growth is not a simple extrapolation of existing trends but continually finds novel directions. This is a core reason why the process seems unbounded and creative. Any theory of increasing complexity must accommodate not just increases in degree but changes in kind. Our hypothesis does so by focusing on functional information and selection: these can apply in any space of configurations, and as new functions arise, the same principle (selection increases FI) applies to those new functions, thus seamlessly carrying the arrow of complexity into new domains.

Implications for Extraterrestrial Life and the Nature of Consciousness

Finally, we consider two domains where our hypothesis bears significant implications: the search for extraterrestrial life/intelligence and our understanding of consciousness. These are naturally speculative topics, but a unified perspective on complexity can provide insight into what we might expect in the cosmos and how we might situate consciousness in the continuum of complexity.

Extraterrestrial Life and Intelligence:

If the increase of complexity is a general trend given the right conditions, then one might argue that life – as a high complexity phenomenon – could emerge on other planets where conditions allow, and potentially progress towards higher complexity (intelligence, technology) as it did on Earth. This touches on the famous Drake Equation factors: probability of life, probability of intelligence, etc. Our hypothesis suggests that if life gets started (a big if), then the drive toward complexity via selection could make the emergence of more complex and eventually intelligent forms more likely than pure chance would indicate. In other words, there may be a kind of “cosmic imperative” for complexity (a phrase associated with biochemist Christian de Duve, who argued life is a cosmic imperative, not accident).

One tangible application is in biosignature and technosignature searches. Researchers like Walker and Cronin have proposed complexity-based metrics to detect life in chemical data. For example, Assembly Theory applied to molecular analysis: if you find a lot of complex molecules on an alien planet (with high molecular assembly index that would be very unlikely without some biological process), that’s a sign of life. This approach stems directly from the idea that life – through selection – produces combinations of atoms that random chemistry wouldn’t. For instance, oxygen in an atmosphere is a simple biosignature; but a more general one might be an anomalously high Shannon complexity in atmospheric composition, or detection of very complex organic molecules (like proteins or weird polymers) that imply many bits of functional info went into making them. NASA and others are interested in general “agnostic biosignatures” (signs of life not tied to specific known biology) – complexity is a prime candidate, either in chemical complexity or entropy reduction patterns.

If complexity tends to rise, then intelligence and technology might be common outcomes on planets that remain habitable for long times. The “Great Filter” hypothesis in SETI discussions wonders if some step (like origin of life or jump to intelligence) is extremely improbable. Our narrative suggests that many steps (like eukaryotes, multicellularity, etc.) were improbable but eventually happened due to the drive of selection and maybe some luck. If EarthExtraterrestrial Life and Intelligence: If the drive toward complexity is truly universal, it lends weight to the idea that life (and eventually intelligence) could emerge on other worlds given the right conditions. In other words, complexity might be the rule, not the exception, whenever physics provides a conducive environment (stable energy gradients, rich chemistry, enough time). One implication is for how we search for extraterrestrial life. Traditional biosignature approaches look for specific molecules (like oxygen, methane imbalance, etc.), but a complexity-centric approach suggests looking for signs of unusual order or information-rich patterns. For example, recent work on assembly theory proposes that we quantify the complexity of molecular assemblages in, say, an alien planet’s atmosphere or rocks. A high molecular assembly index (indicating a molecule that requires many sequential steps to build) could be a smoking gun for life, since non-biological processes rarely produce very complex molecules in significant abundance. In essence, life’s hallmark is improbable configurations (high functional information) made common. NASA scientists have begun considering such complexity measures as “agnostic biosignatures” – indicators of life that don’t assume a particular biochemistry, only an unexpected level of complexity in the chemical makeup. If we detect a chemical system far out of equilibrium with many intricate molecules, it would strongly hint at an evolutionary process at work.

Furthermore, if the law of increasing functional information holds, then on any planet where life begins, one might expect a progression toward greater complexity (barring catastrophe or stagnation). While the timeline can be slow and contingent, this view is cautiously optimistic that simple life, if common, could often evolve complexity, intelligence, and even technology given enough time and stable conditions. This relates to the Fermi Paradox (“Where is everyone?”): if the arrow of complexity tends to produce intelligent, technologically capable species, perhaps such species are not extremely rare. Our framework doesn’t solve the paradox but suggests we should at least expect complexity to appear elsewhere, meaning the absence of evident galactic civilization might be due to other factors (distance, timing, self-destruction, etc.), not a lack of life’s emergence.

Interestingly, thinking of advanced extraterrestrial beings as part of this cosmic complexification can reframe our perspective. Rather than seeing intelligence as a random fluke, we can consider it a natural outcome of evolution’s drive toward new functional domains. On Earth, one lineage achieved a high level of cognitive complexity (humans); on another planet, it could be another organism. The specifics will differ, but under our hypothesis the broad pattern of growing information-processing capability might be common. This means that the search for technosignatures (signals of technology, like radio emissions or artificial structures) is a logical extension of the search for complexity: technology is an off-the-chart complexity phenomenon (consider the organized complexity of a city or a computer network, which far exceeds that of a jungle or a microbial mat). A sufficiently complex biosphere may eventually reshape its planet (e.g., Earth’s city lights, or excess heat, or atmospheric pollutants could be noticed from afar as signs of an intelligent civilization). Thus, our hypothesis supports a multidisciplinary SETI approach: looking for any anomalies of order, from molecular to planetary scale, as potential evidence of life’s handiwork.

The Nature of Consciousness:

Consciousness is arguably the most intricate phenomenon we know, arising from the coordinated activity of billions of neurons. Many theories of consciousness suggest complexity is a key ingredient – notably, the Integrated Information Theory (IIT) posits that consciousness corresponds to the amount of integrated information (denoted $\Phi$) in a system. Indeed, the intuition that consciousness and complexity go hand in hand has driven the popularity of IIT, which essentially quantifies how much a system’s parts act in an irreducibly unified, informationally rich way. In our framework, consciousness can be seen as an emergent property that appears when biological complexity (particularly information processing and integration capability) crosses a certain threshold. The brain is a product of evolutionary selection for complex information processing, so it is no surprise that at some point it developed self-modeling and subjective experience.

If we treat consciousness as part of the continuum of complexity, some implications follow:

• Consciousness is not a mysterious add-on, but a natural outcome of increasing functional complexity in neural systems. It likely gradually increased in our lineage (animals have varying degrees of neural complexity and likely varying degrees of consciousness). The “arrow of complexity” in brains, from simple nerve nets to complex layered cortices, correlates with the richness of subjective experience and cognitive ability.
• This suggests that on other planets, if evolution produces animals with complex brains, it may also produce consciousness. In that sense, consciousness might abound in the universe wherever life becomes complex – a philosophical stance that contrasts with seeing consciousness as exceptionally rare or unique to humans. It resonates with Teilhard de Chardin’s idea of a complexity-consciousness law that as matter complexifies, it becomes inwardly aware.
• The link between functional information and consciousness could be formalized: perhaps consciousness requires a system to integrate a large amount of information (which is a functional demand for certain cognitive tasks). So as evolution selects for higher cognitive function (for example, better predictive modeling of the environment, social intelligence, etc.), it inadvertently pushes systems toward architectures that also maximize integrated information, thus yielding consciousness as a by-product or concomitant property.
• This perspective might guide artificial intelligence research as well: if we create systems of sufficient complexity and integration, they may by the same principles exhibit consciousness or something akin to it. Already, AI systems are growing in complexity (though their architecture is different from brains). IIT would predict that at some point an AI’s $\Phi$ could be non-zero and possibly significant, implying some level of experience. Our hypothesis doesn’t directly address machine consciousness, but it fits the notion that there is no sharp divide: any system (biological or artificial) with enough complexity and the right organization might develop consciousness.

There is also a reflective aspect: humans, as conscious agents, are now deliberately managing complexity. We use our understanding to create more complexity (technology, social systems) – essentially, we have become active drivers of the complexification process rather than passive products. This raises ethical and philosophical questions: if the “law” is to increase complexity/functional information, should we consider consciously steering it (for instance, spreading life beyond Earth to propagate complexity)? Some thinkers have mused that the destiny of intelligent life might be to help the universe generate even more complexity (through projects like megastructures, computational networks, etc.), effectively accelerating the universal complexification. While speculative, it casts human creativity and curiosity as part of a larger cosmic trend.

In summary, considering consciousness in the complexity framework demystifies it somewhat – it becomes the highest known rung (so far) on a ladder of complexity, expected to occur under broad evolutionary conditions rather than a miraculous singularity. It also highlights that as complexity increases, entirely new qualities (like subjective awareness) can emerge that were absent at lower levels – a humbling reminder of the creative power of evolution.

Implications and Predictions

Bringing the threads together, we can outline several broad implications of the hypothesis of universally increasing complexity, as well as some testable predictions or guiding expectations for future research:

Unification of Sciences:

If complexity increase is a unifying trend, we should seek unifying principles that apply across physics, chemistry, biology, and even social sciences. The concept of functional information and selection might serve as such a principle. One prediction is that disciplines will increasingly borrow tools from each other (as we see with information theory in biology, or evolutionary algorithms in engineering) because they are tapping into the same underlying logic of complexification. We might predict the rise of more explicitly interdisciplinary fields (like astrobiology, artificial life, complexity economics) that use evolutionary complexity as a framework.

Detectability of Life and Intelligence:

As mentioned, one practical prediction is that life elsewhere, if it exists, will produce measurable complexity signatures. Missions might soon test this by analyzing Mars samples or the plumes of Enceladus and Europa for unexpectedly complex organic assemblages. A positive detection – say, a set of polymers with very high informational complexity on Enceladus – would strongly support our view that life (complex systems) emerge given the chance. Similarly, in SETI, a continued silence could suggest either that our assumptions are wrong or simply that we haven’t recognized the forms of complexity (e.g., maybe extraterrestrial intelligence doesn’t use radio but we might find evidence in astrophysical data of engineered structures – another form of high complexity).

Future of Complexity on Earth:

If there is a “law” driving complexity, one can ask about the future trajectory on our planet. One implication is that barring catastrophic setbacks, we might expect complexity to keep rising, now mostly in the form of our technology and social organization. This could mean increasing integration of biological and artificial systems (as hinted by the concept of a future “bio-digital fusion” in the figure above). It may also mean new major transitions are ahead – perhaps the emergence of a global brain (the internet plus humanity functioning as a super-organism of sorts) or the integration of human and AI intelligence. While speculative, these are essentially continuations of the pattern of cooperative integration at higher levels. A prediction here is that isolated, simple systems (like individual devices or individual humans) will become ever more networked into larger complex systems (already happening with IoT and global communications). Complexity is shifting from the biological substrate to a mixed bio-tech substrate.

Limitations – The Need for Sustainment:

An important implication is that while complexity can increase, it requires an energy throughput and relative stability. This underscores the importance of sustaining our planet’s habitability. If we prematurely cut off our energy flux (e.g., via nuclear winter or ecological collapse), we could break the trend locally. The Second Law guarantees entropy increase, but the complexity “law” only holds if we manage not to destroy the prerequisites (it’s a conditional tendency, not an absolute necessity). Thus, one might argue that from a cosmic perspective, maintaining conditions for complexity to thrive (e.g., mitigating existential risks) is aligning with the universe’s creative flow. Conversely, self-destruction would be a tragic interruption of a 4-billion-year complexification on Earth.

Philosophical Outlook:

The hypothesis lends itself to an almost narrative view of the universe: from simple beginnings towards ever more complex and capable forms, possibly culminating (far in the future) in intelligence spreading through the galaxy or the universe becoming self-aware through its constituents. This is reminiscent of ideas like the Omega Point (Teilhard or Tipler) – though those are highly speculative, our discussion makes it a scientifically grounded possibility (albeit not inevitable or provable yet). A more immediate philosophical implication is epistemological humility: since complexity can always increase and create new emergent phenomena, we may never have a final, closed understanding of all that can happen. There will always be “new things under the sun” as the proverb goes – a moving frontier of novelty.

Testing the “Law”:

Ultimately, for the law of increasing functional information to gain acceptance, it will need to be tested and quantified in various domains. Predictions here include:

• In laboratory origins-of-life experiments, if we set up many experiments with variation and selection (e.g., continuously stirred reactor with energy input and a selection threshold like a filter or substrate replenishment favoring certain outputs), we should observe a rise in FI of molecules over time, essentially witnessing increasing complexity in a purely chemical system.
• In computer science, open-ended evolutionary algorithms should, if properly implemented, keep generating novel, more complex solutions. A failure to do so might indicate we’ve missed some ingredient (maybe our digital systems lack the richness of physical systems).
• In the fossil record and future monitoring of ecosystems, we might measure functional diversity or information content of genomes and see an increasing trend (for instance, average genome length or regulatory complexity in certain lineages over millions of years).
• On the flip side, the law would predict that in a static environment with no selection pressure, complexity will not increase and may even drift to simplicity. This could be tested with digital life: run one set of simulations with selection for function, and another neutrally – the selected ones should accumulate FI, the neutral ones should not (they might just accumulate neutral mutations which don’t increase functional info).

If these tests consistently support the idea, then we can be more confident that complexity’s increase is as fundamental a part of cosmic evolution as entropy increase – just operating under different conditions.

In conclusion of implications: embracing a universal complexification perspective encourages a hopeful outlook – it portrays life and intelligence as emergent, expected phenomena given the right circumstances, and suggests that what we do (in science, technology, etc.) is part of a deep cosmic trend. It also sets a research agenda: to further uncover the quantitative laws of complexity, to search for life in the universe with an eye for complexity signatures, and to carefully manage our own increasing complexity on Earth.

Limitations and Open Questions

No grand hypothesis is complete without acknowledging its limitations and the open questions that remain. While we have made a case for a universal trend of increasing complexity, several challenges and uncertainties must be considered:

Definition and Measurement Ambiguity:

Complexity is notoriously hard to define in a single universal way. We adopted functional information as a rigorous measure, but even that requires specifying a function and context. One limitation is that in some systems it might be unclear what the relevant function is (e.g., is the function of the biosphere simply to dissipate solar energy? Or something like “persist and reproduce”?). Different choices can yield different assessments of FI. Open question: Can we identify canonical functions for complex systems that allow objective cross-comparison of FI? Additionally, not all forms of complexity are easily measured in practice – algorithmic complexity is uncomputable for large systems, and even FI may be impractical to compute for, say, an entire cell. We often must rely on proxies (like genome length, network connectivity, etc.). There is ongoing work to refine complexity metrics and apply them, but it remains a challenge to quantify claims like “organism A is more complex than organism B” in a rigorous way that correlates with our intuitive and functional sense of complexity.

Counterexamples and Plateaus:

There have been periods where complexity did not noticeably increase or even decreased. For nearly 2 billion years, life on Earth was microbial and seemingly stagnant in terms of major innovation (though microbes were evolving new metabolisms, the morphological complexity plateaued). Some argue that much of life’s history was dominated by relatively simple forms, and only recently has complexity accelerated – thus, complexity increase might be a biased view focusing only on certain lineages (like animals or humans). Stephen Gould pointed out that bacteria are still hugely successful and haven’t been superseded by complexity; in fact, the most fundamental level of life (biomass, biochemical diversity) is still dominated by “simpler” organisms. This raises the question: is increased complexity a necessity or just one strategy among many? Our hypothesis would respond that complexity is not necessarily favored in every environment – it’s favored in niches where function can be improved by it (often in more variable or competitive environments). Meanwhile, in very stable, simple niches, simpler life persists (a bacterium in a thermal vent has no need to become an elephant). Thus, complexity’s arrow is most evident when looking at the envelope of maximum complexity over time, not uniformly across all life. An open research question is to study the conditions under which complexity plateaus versus those where it takes off. For example, did eukaryotes arise only after oxygen rose to a sufficient level? Is there a “tipping point” in environmental complexity that triggers biological complexity to escalate? Understanding such thresholds could refine the “law” to specify when it applies.

Role of Chance:

Major transitions may depend on rare stochastic events (like the endosymbiosis that gave rise to eukaryotes). If that event hadn’t happened, perhaps Earth’s biosphere would still be largely microbial (some argue this). So one could ask: is complexity’s rise inevitable or did we just get lucky a few times? Our perspective leans toward inevitability given enough time – perhaps if one symbiosis hadn’t happened, another route to complexity would have eventually arisen (e.g., through different symbioses or gene transfers). But this is not proven. It could be that in the majority of biospheres, life stalls at a relatively simple stage because certain key innovations are very low-probability. This is directly related to the Great Filter hypothesis in astrobiology. Open question: what are the probabilities of those key transitions? This could be informed by examining multiple independent lines of evolution on Earth (e.g., multicellularity evolved many times – suggesting it’s not extremely improbable; but eyes or intelligence evolved fewer times, though still more than once in the case of eyes). If we had data from multiple planets, we could start to answer this statistically, but we currently have a sample size of one. Until then, the inevitability vs. contingency of complexity’s increase remains debated.

Second Law Constraints and Energy Supply:

While complexity can locally decrease entropy, it requires an energy source to do so. Planetary systems have finite lifetimes; as the Sun ages, Earth will lose habitability, presumably cutting off further complexity here. On cosmic scales, star formation will cease billions of years from now and the universe will trend to heat death. Thus, one limitation is that the complexity trend has a window of opportunity. It’s not eternal – eventually, increasing entropy will dominate as usable energy runs out. There is an open question about how far complexity can go before those ultimate limits halt it. Freeman Dyson speculated about life adapting to an ever-cooling universe, but physical limits (like the thermodynamic availability of work) impose an asymptotic end. However, that’s trillions of years away; nearer term, one could ask: are there hard plateaus before then? For instance, maybe once intelligence and technology reach a certain point, the next “level” (like perhaps a planet-wide mind or a civilization that manages star energy) might be very hard to achieve due to coordination problems or self-destructive tendencies (some argue humanity is facing such a critical test). So it’s conceivable complexity could stall or collapse if challenges (climate change, war, etc.) are not navigated. Our hypothesis, being descriptive, doesn’t ensure success – it just says if selection for function continues, complexity should rise. If we collectively choose to stop pushing complexity (or inadvertently cause collapse), the “law” would not save us. Thus, it’s only as good as the conditions allow. Studying societies that collapsed (like Easter Island) might offer insight into whether complexity can also unravel under resource constraints, which is a cautionary tale that local countertrends (complex systems collapsing) are very real.

Causality vs. Correlation:

One could ask, does complexity increase because of some underlying principle (as we argue), or simply because of initial conditions and probability (a sort of anthropic observation: we see complexity because we’re results of it, but maybe it’s exceedingly rare overall)? To solidify a law, we need to demonstrate causality: e.g., show that selection necessarily drives FI up under broad conditions. The PNAS 2023 paper by Hazen et al. attempts a theoretical argument for that. Still, more formal work could be done: for instance, proving theorems in evolutionary theory that under certain assumptions, complexity (in some formal measure) will increase. Some work exists (e.g., Fisher’s fundamental theorem of natural selection for fitness, or Price’s theorem), but complexity is trickier than fitness. There’s an open theoretical question: can we derive complexity increase from first principles of non-equilibrium thermodynamics and information theory? Some have tried (Jeremy England’s work on dissipation-driven adaptation is one attempt to derive spontaneous “lifelike” self-organization from physics). The jury is still out on a rigorous derivation.

Alternate Forms of Complexity:

Our discussion largely assumes “Earth-like” evolution. But could there be entirely different routes to complexity? For example, could there be a non-carbon-based form of organized complexity (perhaps plasma life in stars or information life inside computers)? If so, does our hypothesis encompass those? The law of increasing FI in principle is substrate-agnostic (it’s about configurations undergoing selection for function). So it should apply to, say, digital evolution in a computer: indeed, genetic algorithms demonstrate “digital organisms” evolving complexity when set to task. It could also apply to hypothetical plasma creatures (if they have variation and persistence). But without concrete examples, this remains speculative. It is an open question to what extent we can generalize life – this is exactly why NASA wants “agnostic biosignatures” because alien life could be very different. The risk is that our notion of function and selection might be too tied to known chemistry. Part of addressing this is creating artificial life in various media (chemically, electronically) to see if complexity arises similarly. If it does in all cases, that’s strong support; if it only does in very biochemical systems, maybe that hints at some special sauce in chemistry.

Ethical and Philosophical Concerns:

Finally, an open-ended system that increases complexity will eventually raise ethical questions: for instance, if we create increasingly complex (and possibly conscious) AI, how do we regard their moral status? Does the “value” of a system correlate with its complexity (a somewhat perilous idea, as one might misinterpret it as more complex = more worthy; whereas an ant or a bacterium, though less complex, are still unique and important)? Our thesis doesn’t directly tackle ethics, but it implies that complexity is something precious (being rare in the universe and hard-won by evolution). This could inspire a sense of duty to protect and foster complexity (whether biodiversity or human culture or potential future life forms). It’s an open question how to integrate a scientific understanding of complexity with a value system — a domain where philosophy and science need to dialogue.

In summary

While the hypothesis that complexity tends to increase is compelling and supported by many lines of evidence, it is not a simple deterministic law. It is probabilistic, conditional, and contextual. Recognizing its limits – that it requires selection pressures, that it can be derailed by external or internal catastrophes, that it may have exceptions – is important. The open questions identified show a fertile ground for future research: from quantifying complexity rigorously, to exploring evolution in alternate scenarios, to ensuring that humanity’s trajectory continues to follow an upward complexification (rather than a collapse). As with the early days of thermodynamics or evolution theory, we have a guiding idea but much to refine and discover. The coming decades of research – in complex systems science, astrobiology, AI, and evolutionary theory – will likely clarify these issues, either reinforcing the notion of a complexity law or revealing its caveats.

Conclusion

We have traversed a vast landscape of ideas, from the origin of the universe to the workings of the cell, from the mind of an organism to the prospect of alien civilizations, all tied together by a single unifying thread: the tendency for complexity to increase given the right conditions. Our central hypothesis is that complexity – measured in terms of functional information and organized structure – serves as a kind of directional arrow of time in open, evolving systems. It is not a rigid, monolithic arrow like entropy’s increase, but a statistical and opportunistic one, manifest wherever variation and selection allow pockets of order to progressively refine and build upon themselves.

The evidence for this trend appears in multiple arenas. Cosmologically, we see simple particles giving way to stars, planets, and chemistry. Biologically, we see life’s humble start leading to the richness of the biosphere and human intellect. Even in our technology and culture, the acceleration of innovation and interconnectedness points to a continuation of the complexification process. By synthesizing concepts from thermodynamics, information theory, and evolutionary biology, we proposed that a law of increasing functional information might underlie these observations. This law would hold that whenever a system can explore many configurations with feedback (selection) retaining the successful ones, it will accumulate information and become more functionally complex – in effect, it will evolve. Such a principle treats Darwinian evolution as a special case of a broader natural phenomenon that also encompasses chemical evolution, planetary evolution, and even cultural evolution.

We discussed how this hypothesis, if true, has deep consequences. It suggests that life and mind are not accidents but somewhat expected outcomes of the cosmos given enough time and opportunity, thereby bridging the gap between physics and meaning. It offers a framework for searching for life in the universe by looking for complexity itself as the telltale sign. It provides a narrative for humanity as part of a continuum – we are not the end point of evolution but a recent emergence in a long lineage, possibly with much further to go. It also reframes how we view the future: rather than a random walk, there could be a direction (though not a fixed destination) toward more diverse, higher-order forms.

At the same time, we tempered this view with the acknowledgement of randomness, context, and contingency. Complexity’s rise is not guaranteed – it can falter, reset, or take myriad paths. The “law” we speak of is more like a guiding tendency or constraint on the space of possibilities, akin to how the second law constrains thermodynamic processes but does not dictate every detail. There remain many open scientific questions, such as quantifying complexity across domains and understanding the probability of major transitions. This thesis does not claim that all is solved; rather, it lays out a research program and a worldview. The argument-driven inquiry presented here builds the case that increasing complexity is a real and profound aspect of our universe, while also highlighting that our understanding of it is still evolving and incomplete (perhaps inherently so, in a Gödelian twist).

In conclusion, viewing the universe through the lens of increasing complexity enriches our understanding in multiple ways. It provides coherence across levels of organization, seeing a thread from quarks to consciousness. It emphasizes process over static being: a universe in becoming, not just being. It integrates information and function into fundamental physics discourse, hinting that “to exist” in an evolutionary sense is “to perform and persist.” And importantly, it inspires a sense of connection and purpose: we, as complex beings, carry forward the torch of complexity – what we do matters not just to us, but as part of this grand cosmic story of emerging order.

The thesis we have developed is both descriptive and, implicitly, normative: descriptively, it charts what has happened and arguably will continue to happen; normatively, it suggests that fostering complexity (life, knowledge, creativity) is aligned with the grain of the cosmos. Whether or not one accepts the latter sentiment, the former can be investigated with the tools of science. As we stand at the precipice of exploring other planets, creating new forms of life in the lab, and merging technology with biology, the framework of complexity rising will serve as a valuable guide. It reminds us that from a simple Big Bang, a universe capable of contemplating itself has unfolded – and that process may still be nearer its beginning than its end. By continuing to study and respect this fundamental trend, we not only seek knowledge for its own sake but also insight into our own place in the tapestry of existence.

References

• Hazen et al. (2007) – Hazen, R.M., Griffin, P.L., Carothers, J.M., & Szostak, J.W. “Functional information and the emergence of biocomplexity.” PNAS 104, 8574–8581 (2007).
• Hazen et al. (2023) – Hazen, R.M., Wong, J., et al. “On the roles of function and selection in evolving systems.” PNAS 120(15): e2210223120 (2023). Proposal of the “law of increasing functional information” and discussion of selection in physical and biological systems.
• Quanta Magazine (2025) – Powell, D. “Why Everything in the Universe Turns More Complex.” Quanta Magazine, April 2, 2025. Summary of Hazen’s work and perspectives on universal complexity trends.
• Chaisson (2001, 2013) – Chaisson, E.J. “Cosmic Evolution: The Rise of Complexity in Nature.” (Harvard Univ. Press, 2001); and Chaisson, E.J. “Using complexity science to search for unity in the natural sciences,” in Complexity and the Arrow of Time (Lineweaver et al., eds, 2013). Develops the concept of free energy rate density as a metric of complexity, showing an exponential increase from Big Bang to humankind, and argues that energy flow underlies growing complexity in accord with 2nd law.
• Lineweaver & Egan (2008) – Lineweaver, C.H. & Egan, C.A. “Life, gravity and the second law of thermodynamics.” Physics of Life Reviews 5, 225–242 (2008). Discusses how entropy increase is compatible with local complexity (life) and proposes that life is a natural byproduct of thermodynamic imperatives (uses Earth’s history as example).
• McShea & Brandon (2010) – McShea, D.W. & Brandon, R.N. “Biology’s First Law: The Tendency for Diversity and Complexity to Increase in Evolutionary Systems.” (Univ. of Chicago Press, 2010). Argues for a default tendency of complexity (especially morphological complexity) to increase in evolution, absent strong constraints. Offers theoretical underpinning for a passive trend of increasing complexity.
• Maynard Smith & Szathmáry (1995) – Maynard Smith, J. & Szathmáry, E. “The Major Transitions in Evolution.” (Oxford Univ. Press, 1995). Identifies the major evolutionary transitions (genome integration, eukaryosis, multicellularity, etc.) and discusses how each involves new levels of organization and information transmission.
• Longo, Montévil & Kauffman (2012) – Longo, G., Montévil, M., & Kauffman, S. “No entailing laws, but enablement in the evolution of the biosphere.” (Preprint arXiv:1210.5908, 2012). Philosophical paper arguing that evolution is not fully described by fixed laws due to continual introduction of novelty (uses analogies to Gödel’s theorem).
• Walker et al. (2023) – Sharma, A. et al. (including S.I. Walker, C. Kempes, M. Lachmann, L. Cronin). “Assembly theory explains and quantifies selection and evolution.” Nature 622, 321–328 (2023). Introduces Assembly Theory as a way to quantify object complexity by the length of assembly pathway, and connects it to selection processes. Suggests a new framework bridging physics and biology, with an eye towards detecting life via molecular complexity.
• Gillings et al. (2016) – Gillings, M.R., Hilbert, M., & Kemp, D.J. “Information in the Biosphere: Biological and Digital Worlds.” Trends Ecol. Evol. 31(3): 180–189 (2016). Discusses the exponential growth of information produced and stored by biological and digital systems, drawing parallels between genetic information increase over evolutionary time and digital information explosion. (The figure used is based on concepts from this paper.)
• Veit (2022) – Veit, W. “Consciousness, complexity, and evolution.” Behav. Brain Sci. 45:e61 (2022). Commentary on the relationship between evolutionary complexity and consciousness, noting the intuitive appeal of integrated information theory in linking high complexity with the emergence of consciousness.
• Integrated Information Theory – Oizumi, M., Albantakis, L., & Tononi, G. “From the phenomenology to the mechanisms of consciousness: Integrated Information Theory 3.0.” PLoS Comput. Biol. 10(5): e1003588 (2014). (Not directly cited above, but foundational to the idea that consciousness corresponds to integrated information, providing context to our discussion on consciousness and complexity.)
• Miscellaneous: Additional sources and references are embedded in the text via bracketed citations, indicating specific supporting evidence (e.g., data from PNAS articles, statements from Quanta Magazine, or Wikipedia summaries of known scientific concepts). These include direct quotations or data about functional information, the formulation of the complexity law, mineral evolution and selection analogies, assembly theory and life detection, and others as noted in the text. Each such citation points to the source and line numbers for verification.