Table of Contents
Abstract
Background: The stepped-wedge cluster randomized trial (SW-CRT) is a type of cluster-randomized study design in which all clusters (e.g. hospitals or communities) eventually receive the intervention, but the timing of rollout is randomized in a staggered, stepwise fashion. This design has gained prominence for evaluating health service interventions when logistical, ethical, or practical constraints prevent simultaneous rollout. We introduce the SW-CRT’s origins and conceptual underpinnings, contrasting it with traditional parallel cluster randomized trials.
Methods: We review critical statistical features of SW-CRTs, including control for secular trends (time effects) and accounting for intra-cluster correlation. Classical SW-CRT analyses assume an immediate and constant treatment effect post-intervention; we discuss the assumptions and potential pitfalls of this assumption, highlighting recent methodological research (notably by James Hughes and colleagues) that examines time-varying treatment effects. A detailed statistical methods section is provided, describing the model structure, design matrix formation, incorporation of time effects, intracluster correlation considerations, power and sample size calculations, and emerging analytic methods that relax the constant-effect assumption. Technical sections are marked for readers who wish to skip detailed statistical derivations.
Results: The role of SW-CRTs in clinical research and implementation science is explored, with a focus on their growing use in global health settings. As a central case study, we examine a SW-CRT conducted in Mozambique’s antenatal care (ANC) clinics. In this trial, provision of medical supply kits was introduced to 10 clinics in a random sequence to improve the quality of ANC. We describe its design, implementation, and outcomes. The intervention led to immediate and sustained improvements in key ANC practices, including screening for anaemia and proteinuria and provision of prophylactic deworming, under routine care conditions. We cite the trial protocol, dataset sharing protocol, and the Lancet Global Health publication to detail these findings.
Discussion: We interpret the Mozambique trial results and illustrate why the SW-CRT design was particularly valuable: it allowed rigorous testing of an intervention during routine service delivery without depriving any cluster of the intervention in the long run. We discuss how using routine health system data in SW-CRTs can enhance external validity and facilitate pragmatic implementation research, especially in low- and middle-income country (LMIC) settings. The SW-CRT’s strengths (e.g. ethical acceptability, ability to adjust for time trends) and challenges (e.g. longer study duration, complex analysis) are critically examined. We also summarize recent innovations in SW-CRT methodology that address delayed or time-varying intervention effects.
Conclusions: The SW-CRT is a robust and increasingly important design for evaluating health interventions in real-world settings. It supports evidence-based policymaking by generating high-quality evidence under pragmatic conditions. We offer a dedicated section for health policy makers, written in accessible language, to highlight why SW-CRTs are useful for health policy, how they support decisions with strong evidence, and what practical insights the Mozambique case study provides. In conclusion, SW-CRTs enable the ethical and efficient evaluation of interventions at scale, and ongoing methodological advancements continue to strengthen their validity for guiding health policy and practice.
Introduction
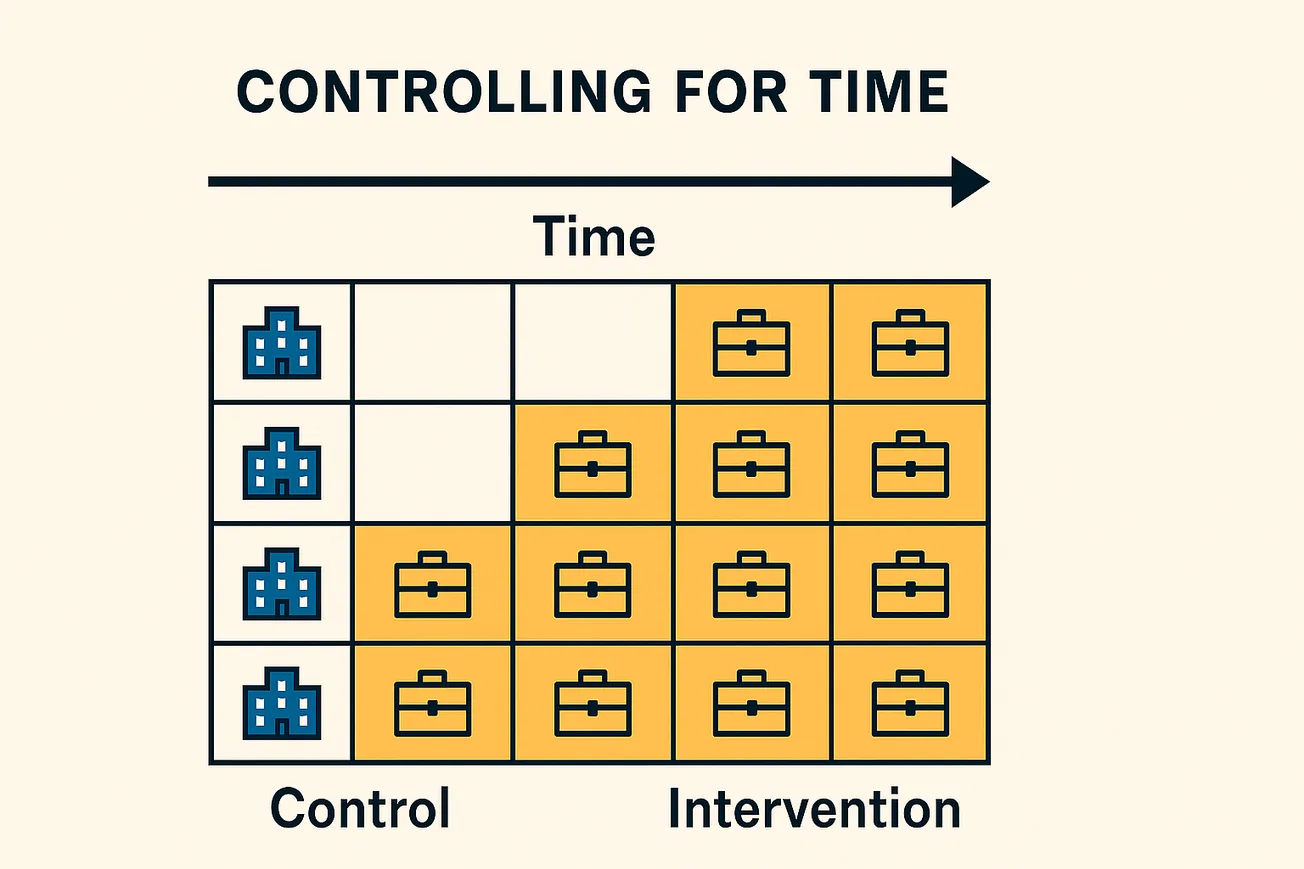
Randomized controlled trials (RCTs) are the gold standard for evaluating interventions, but practical constraints often arise in real-world settings that make traditional trial designs infeasible or ethically problematic. The stepped-wedge cluster randomized trial (SW-CRT) has emerged as an innovative trial design that addresses some of these challenges. In a SW-CRT, clusters (such as hospitals, clinics, or communities) are randomized to different time points at which they transition from control to intervention, in a staggered sequence. By the end of the study, all clusters will have received the intervention, but the order and timing of rollout is randomized. Figure 1 illustrates a stepped-wedge schedule for 10 clusters across 10 time periods:
Figure 1. Example of a stepped-wedge cluster randomized trial design. Each cluster begins in control (C) and switches to treatment (T) at a randomized period. By the final period, all clusters are receiving the intervention.
The SW-CRT was first employed in the mid-1980s in a landmark trial: the Gambia Hepatitis B vaccine study, which phased in vaccination across communities to evaluate its impact on liver cancer and chronic liver disease. The term “stepped wedge” derives from the visual depiction of clusters switching to the intervention sequentially, resembling a stair-step pattern of intervention allocation over time. The design was conceptually anticipated by methodological authors such as Donald Campbell and colleagues in the 1960s–70s, who discussed staged introduction of interventions when simultaneous implementation is not possible.
Comparison to Traditional Designs: In a traditional parallel cluster randomized trial, clusters are randomly allocated to intervention or control at the trial start, and some clusters may never receive the intervention. By contrast, a SW-CRT is a type of one-directional crossover design: every cluster provides data under control and, later, under intervention conditions (i.e., each cluster acts as its own control over time). This has two important implications. First, from an ethical standpoint, if there is preliminary evidence or strong belief that an intervention will likely do more good than harm, stakeholders may be reluctant to withhold it entirely from any group. The stepped-wedge design addresses this by eventually delivering the intervention to all clusters, which can be morally and politically appealing in contexts such as public health programs or policy interventions. Second, from a logistical perspective, resource or infrastructure limitations often mean an intervention cannot be rolled out everywhere at once. The stepped-wedge design accommodates phased implementation due to staffing, funding, or supply constraints by design. In the Mozambique antenatal care trial we will examine, for example, the intervention (a package of antenatal care improvements) could only be implemented in stages due to logistical and financial constraints, and the order of rollout was randomized to ensure fairness and rigor.
Development of the SW-CRT: After the Gambian hepatitis study, use of SW-CRTs remained relatively infrequent for some time, but the design attracted increasing interest in the early 2000s. Methodologists began to formalize its properties; Michael Hussey and James Hughes (2007) provided one of the first comprehensive discussions on the design and analysis of stepped-wedge cluster trials. A systematic review by Brown and Lilford (2006) catalogued early examples and motivations for using stepped wedges. Common reasons included: (1) Ethical obligation – ensuring all groups eventually receive the presumably beneficial intervention; (2) Practical constraints – inability to deliver the intervention simultaneously to all clusters due to limited resources or logistical complexity; (3) Scientific advantages – ability for clusters to act as their own controls and to adjust for underlying time trends in outcomes.
At the same time, researchers noted challenges of the SW-CRT. By necessity, SW-CRTs usually require a longer study duration than a parallel trial, since clusters must wait their turn to receive the intervention. This prolongation can introduce issues if underlying conditions change substantially over time (e.g. secular trends in the outcome due to unrelated factors or evolving external influences). Additionally, because the intervention is rolled out openly, it is often impossible to blind participants or providers to intervention receipt. Blinding outcome assessors and maintaining uniform data collection become critical to mitigate bias. Contamination (interaction between clusters that have received the intervention and those that have not yet) is another concern, requiring adequate geographic or organizational separation or careful implementation to prevent spillovers. Despite these challenges, the design’s appeal has led to rapid uptake. In recent years, its use has “increased rapidly” in fields like health services and implementation research. One review identified 160 SW-CRTs published between 2016 and 2022, demonstrating that it is no longer a niche design but a mainstream option for trialists.
In the following sections, we delve deeper into the statistical aspects of SW-CRTs (with technical details provided for interested readers), then explore the application of the design in a real-world trial in Mozambique. We also discuss the relevance of SW-CRTs in implementation science and global health, where their ability to generate evidence without disrupting ongoing services is particularly valuable.
Literature Review
Conceptual Underpinnings of the Stepped-Wedge Design
The SW-CRT is conceptually rooted in cluster randomized trial methodology and crossover designs. A cluster randomized trial (CRT) is one in which intact groups of subjects (clusters), rather than independent individuals, are randomized to intervention or control. This design is often preferred when individual randomization is impractical (for example, an intervention like a new clinical protocol must be applied to an entire clinic) or when we want to avoid “contamination” (the influence of an intervention on nearby control individuals, which can occur if both groups exist in the same social or physical space). CRTs have been used to evaluate public health and service delivery interventions such as educational programs, infection prevention strategies, and community health policies. A critical statistical feature of CRTs is that outcomes of individuals within the same cluster tend to be correlated – an aspect measured by the intra-cluster correlation coefficient (ICC). The ICC represents the proportion of total outcome variance that is attributable to differences between clusters rather than between individuals. Any analysis or sample size calculation for CRTs must account for this within-cluster correlation; failure to do so will understate uncertainty and overestimate effective sample size.
The stepped-wedge design is a type of cluster trial where clusters cross from control to intervention sequentially. Unlike a standard crossover where clusters might switch back and forth or where only a subset crossover, the SW-CRT features a unidirectional switch (once a cluster begins the intervention, it usually continues with it for the remainder of the study). All clusters start in the control condition, and by the end, all are in the intervention condition, with different clusters having different lengths of exposure to the intervention. This structure inherently requires multiple observation periods (time is divided into steps or periods) and careful scheduling. The number of steps (periods at which new clusters crossover) can vary: some trials might have only a few steps (with large increments of clusters switching at once), whereas others have many steps (one cluster switching at a time in many small increments). A minimum of two steps (one crossover point) is required to be considered a stepped wedge; some argue that more steps (three or more) are preferable to truly leverage the design’s strengths. More steps generally allow finer control for time trends and more gradual accumulation of intervention exposure data, but they also prolong the trial.
Control for Time (Secular Trends): A major scientific rationale for SW-CRTs is the ability to separate intervention effects from secular trends in the outcome. In public health and clinical research, background factors (e.g., seasonal variations, policy changes, gradual improvements in care over time) can cause outcome rates to change independently of the intervention. A parallel cluster trial cannot easily distinguish whether an observed difference between groups is due to the intervention or due to underlying changes over time, especially if the trial is long. The stepped-wedge design, however, because of its staggered rollout, has clusters observed under control and intervention conditions at various time points throughout the study. The built-in time stratification means that at any given time during the trial, some clusters are still in control while others are in intervention, allowing an adjustment for temporal trends when comparing outcomes (The stepped wedge trial design: a systematic review | BMC Medical Research Methodology | Full Text). Essentially, time becomes an adjustable factor in the analysis model (usually as fixed effects for each period), so that any overall improvement or decline in outcomes over the calendar time of the study is accounted for, preventing a biased attribution of those trends to the intervention. Brown and Lilford noted this advantage in their review, citing that a stepped wedge “offers an opportunity to measure possible effects of time of intervention on the effectiveness… [and] to detect underlying trends/control for time” as a scientific motivation for the design.
Ethical and Political Acceptability: As introduced, a key reason to use a SW-CRT is when there is a feeling that withholding an intervention would be unethical or unacceptable, yet immediate full rollout is not feasible. In such cases, a randomized stepped rollout can be a fair way to allocate the timing of the intervention. All clusters are assured to eventually get the intervention (addressing “fair access” concerns), but the staggered start times allow the researchers to use a randomized controlled framework to evaluate impact. This feature can be especially pertinent in trials of service delivery or policy changes in health systems. For example, if a new treatment guideline is believed to save lives, it may be deemed unethical to randomize some hospitals to never implement it. But a stepped-wedge trial could implement the guideline in all hospitals, just not all at once, providing the needed comparison of outcomes before vs. after implementation under randomization. In the Mozambique antenatal care trial (detailed later), stakeholders felt it would be politically and ethically difficult to exclude some clinics from receiving an intervention aimed at improving quality of care. The stepped-wedge approach was chosen to ensure all clinics would receive the intervention by trial’s end.
Practical Considerations: Many SW-CRTs are conducted in settings where rolling out an intervention incrementally is the only practical option. This could be due to resource constraints (limited supply of intervention materials or trainers, budget that only supports gradual implementation) or due to the need to learn and adapt as one scales up (for complex interventions, implementers might prefer to pilot in a few sites, then extend to others in waves). The stepped-wedge design aligns with these scenarios, as it essentially formalizes a phased implementation into an experimental design. From a recruitment and stakeholder engagement perspective, the knowledge that one’s site will eventually get the intervention can enhance cooperation and willingness to participate – clusters are not “sacrificed” to permanent control status. However, it must be acknowledged that SW-CRTs usually run longer than equivalent parallel trials and require sustained commitment from all sites (since even control data collection continues until each site’s turn for the intervention arrives).
Critical Statistical Features of SW-CRTs
Intra-Cluster Correlation (ICC): Like any cluster trial, SW-CRTs must contend with intra-cluster correlation. If patients within the same clinic tend to have more similar outcomes (due to shared staff, environment, or population), the effective sample size is reduced compared to an individually randomized trial. The design and analysis must account for this by using appropriate models (see Methods) and usually by inflating sample size (number of clusters or observations) during planning to achieve adequate power. In the Mozambique ANC trial, for instance, an ICC of 0.05 was assumed in sample size calculations. This ICC implies that 5% of the variation in the ANC quality outcomes is due to differences between clinics, and the remainder due to differences between individual visits or patients. Adjusting for ICC often means we need more total patients/observations than if responses were independent. Hussey and Hughes (2007) provided formulae for variance of treatment effect estimates in SW-CRTs, which in turn feed into power calculations. One key insight is that SW-CRTs can sometimes achieve higher power than a parallel CRT with the same number of clusters, because each cluster contributes data to both control and intervention conditions (in effect, each cluster serves as its own control to some extent, reducing between-cluster variability in the treatment effect estimate). However, this benefit can be offset by the design’s longer duration and the need to model time effects. Designing an efficient SW-CRT thus involves a careful balance of number of clusters, number of steps, cluster size (observations per period per cluster), ICC, and desired effect size. Recent extensions by Hemming and colleagues have provided refined power calculation methods for variations of the stepped wedge (e.g., unequal cluster sizes, different link functions for outcomes).
Secular Trend (Time Effect) Control: By design, SW-CRTs incorporate time as an explicit factor. Most analyses will include fixed effects for each time period (or a similar adjustment, like a continuous time trend if appropriate) to capture the underlying secular trend. This is critical: it means that the comparison of intervention vs. control is made after adjusting for any general improvement or change that would have happened over time even without the intervention. In other words, the staggered rollout “mixes” intervention and control observations across the calendar timeline of the study, allowing the model to distinguish intervention impact from temporal changes (The stepped wedge trial design: a systematic review | BMC Medical Research Methodology | Full Text). Control for time is a major advantage of the stepped wedge, as noted, but it requires the correct specification of those time effects in the model. Typically, period fixed effects are used (one indicator for each distinct time period in the study, analogous to a stratification by time). Alternatively, if there is reason to assume a smooth trend, a parametric form (like linear or quadratic trend) could be used, but misspecification risk is higher. Standard practice is to use period fixed effects as a flexible way to capture any pattern of change over time. We will see in the case study that the Mozambique trial spanned 22 months; any secular improvements in ANC practices due to nationwide policy or other factors would be adjusted out by including time effects in the analysis.
Assumption of Immediate and Constant Treatment Effect: A classical assumption in many SW-CRT analyses is that once a cluster initiates the intervention, the effect on outcomes is immediate and then remains constant thereafter. In other words, the model often posits a single intervention effect parameter that applies uniformly to all post-intervention observations in a cluster, regardless of whether it’s right after rollout or much later. Under this assumption, data from a cluster contribute to estimating the same intervention effect whether they were observed just after the cluster started the intervention or long after. This simplifying assumption is convenient and is used by default in many power calculations and analysis plans (it is sometimes called the “canonical” or “immediate-and-constant effect” assumption). It implies, for example, that if an intervention is introduced at a clinic, the clinic’s outcome jump (improvement) is fully realized in the very next period and stays at that new level; any delay or gradual ramp-up is ignored.
However, this assumption may be unrealistic in certain implementations. The effect of an intervention might increase or decrease over time after introduction – for instance, there might be a learning curve (effects grow as staff become more adept) or a waning adherence (effects diminish as enthusiasm or resources fade). If the intervention effect is not truly constant over time, an analysis that forces a single constant effect estimate could be biased. Recent methodological research by Hughes and others has highlighted this issue: if one erroneously assumes a constant effect when the effect actually varies with exposure time, the estimate of treatment effect can be misleading. In fact, Kenny et al. (2022) demonstrated that under time-varying effects, the usual SW-CRT analysis may underestimate or otherwise mischaracterize the intervention’s impact. We will discuss methods to detect and account for time-varying effects in the Statistical Methods section and revisit whether the Mozambique trial showed any time-varying pattern.
Heterogeneity of Treatment Effects: Another aspect to consider is variation in the intervention effect across clusters or contexts. While each cluster eventually gets the intervention, the magnitude of its effect might differ from cluster to cluster (due to differences in population, implementation fidelity, etc.). The SW-CRT, like other multisite trials, can explore this by including interaction terms or random effects for the treatment effect. A straightforward analysis might assume a common effect across all clusters (fixed effect), but advanced models can allow random slopes for the intervention effect. There is a trade-off: allowing heterogeneity (random treatment effects) acknowledges reality but uses up degrees of freedom and can reduce power to detect an average effect. Hughes, Granston, and Heagerty (2015) discuss treatment effect heterogeneity as one of the “current issues” in SW-CRT design and analysis. They point out that one must carefully decide whether the scientific question is about an overall average effect or about cluster-specific effects, and plan the design/analysis accordingly. In many implementation studies, the average effect is primary, but demonstrating consistency (lack of heterogeneity) strengthens generalizability. In the Mozambique case, the authors noted “negligible heterogeneity between sites” in the intervention effect, suggesting the intervention worked fairly uniformly across the different clinics – a reassuring finding for scaling up.
Secular Changes vs. Exposure Time Effects: It is crucial to distinguish two types of time-related effects in SW-CRTs: (1) Secular time effect (sometimes called “calendar time” or “period effect”): this is the effect of time passage during the study, affecting outcomes irrespective of intervention (controlled by period fixed effects, as above). (2) Exposure time (time since intervention) effect: this is how the effect of the intervention changes as more time passes after a cluster begins the intervention. Traditional analysis assumes no exposure-time effect beyond the immediate jump. But if we allow that the effect might depend on how long the intervention has been in place, we then have to model exposure time in addition to calendar time. This complicates the analysis because calendar time and exposure time are partly collinear (later calendar periods tend to include clusters with longer exposure). Nonetheless, sophisticated approaches exist to handle it, which we’ll outline.
In summary, the stepped-wedge CRT comes with a set of assumptions and analytic practices that need to be understood. It controls for secular trends by design (a strength), requires handling of clustered data (like any CRT), and often assumes a constant treatment effect (which may need scrutiny). The literature in the past decade, especially contributions from James P. Hughes and colleagues, has critically examined these features and provided guidance on best practices for design and analysis. We now proceed to an in-depth statistical methods section, which includes technical details on how SW-CRT data are structured and analyzed. Non-specialist readers may skip to the Results or Discussion sections if the upcoming statistical content is too detailed.
Methods (Statistical Methods and Models)
Technical Note: The following section provides a rigorous statistical exposition of the stepped-wedge cluster randomized trial design. It includes model notation, equations, and methodological details intended for readers with a biostatistical background. Non-specialist readers interested primarily in the application and results may proceed to the next section (Results or Discussion) as needed.
Model Structure for SW-CRT Data
Consider a stepped-wedge trial with \(I\) clusters (indexed by \(i = 1, 2, \dots, I\) observed over \(J\) time periods (indexed by \(j = 1, 2, \dots, J\). Without loss of generality, assume one cluster (or a group of clusters) transitions from control to intervention in each period after an initial baseline period. (Some designs have more complex step patterns, but we can always index periods such that each cluster has a defined “transition point.”) Let \(X_{ij}\) be an indicator that cluster \(i\) is under the intervention at time period \(j\). In a perfect stepped wedge, there exists a sequence assignment such that for each cluster \(i\), there is a specific period \(q(i)\) when it switches:
\[Xij= \begin{cases} 0, & j < q(i) \\ 1, & j \ge q(i) \\ \end{cases}\]
with the special case that some clusters might switch at \(q(i)=J+1\) (meaning they only get intervention after study completion, if any cluster remains as a control for entire study – usually not the case in a complete wedge).
Data are collected at the individual level within each cluster-period. Let \(Y_{ijk}\) be the outcome measurement for individual \(k\) in cluster \(i\) at period \(j\). For example, \(Y_{ijk}\) could be a binary indicator of whether a pregnant woman received a certain ANC service (as in our case study), or an outcome like blood pressure reading, etc. The total number of individuals observed in cluster \(i\), period \(j\) can be \(n_{ij}\) (which might be equal for all \(i,j\) in a design with equal cluster-period sizes, or variable in a more pragmatic design).
A common statistical model for SW-CRT outcomes is a generalized linear mixed model (GLMM) that includes:
- Fixed effects for time period (to adjust for secular trends).
- A fixed effect for treatment (often assumed constant across periods once applied).
- Random effects to account for clustering (and possibly additional random effects for between-period variability or other hierarchical structure).
For a continuous outcome (using an identity link, normal errors), one might write:
\[Yijk= \mu + \sum_{j'=1}^{J-1} \gamma_{j'} \cdot \mathbf{1}(j = j') + \theta \, X_{ij} + u_i + \varepsilon_{ij k}\]
where \(\mu\) is an intercept (could be absorbed into the \(\gamma\) for baseline period), \(\gamma_{j'}\) are fixed effects for periods \(2,3,\dots,J\) (with period 1 as baseline reference, for example), \(\theta\) is the intervention effect (assumed constant here for all post-intervention observations), \(u_i\) is a random intercept for cluster \(i\) (to model the intra-cluster correlation), and \(\varepsilon_{ijk}\) is the individual error term. The \(u_i\) are typically assumed i.i.d. normal with variance \(\sigma^2_u\), and \(\varepsilon_{ijk}\) are i.i.d. normal with variance \(\sigma^2\).
For binary or categorical outcomes, a logistic (logit link) or other appropriate link would be used:
\[logit(P(Yijk=1)) = \mu + \sum_{j'=1}^{J-1} \gamma_{j'} \mathbf{1}(j=j') + \theta X_{ij} + u_i\]
This is a generalized linear mixed model with a logit link and random intercept \(u_i\). Typically \(u_i \sim N(0, \sigma^2_u)\) and captures the cluster’s propensity for the outcome. The inclusion of \(X_{ij}\) (treatment indicator) alongside time effects \(\gamma_{j'}\) ensures that the treatment effect \(\theta\) is estimated while controlling for any overall time trend.
Design Matrix Representation: The design matrix for such a model has a distinct block structure. Each cluster contributes \(J\) rows (one per period per cluster, if aggregated outcomes per period, or \(n_{ij}\) rows if individual-level data – but conceptually, we can think at the cluster-period level for design). The treatment indicator column \(X_{ij}\) will be 0 for early periods for that cluster, then 1 thereafter; it is effectively a step function in each cluster’s row block. The time effect columns are identical across clusters – e.g., a column for period 2 has entries 1 for all observations in period 2 (for any cluster) and 0 otherwise. If individual-level data is used, typically the time and treatment indicators are repeated for each individual in a cluster-period, and the cluster random effect links all individuals in a cluster.
A simplified design matrix for a toy SW-CRT with 4 clusters and 5 periods (as per Figure 2) might look like this (showing just fixed effect portions):
Figure 2: Simplified SW-CRT Design Matrix (Toy Example)
| Cluster | Period | Intercept | P2 | P3 | P4 | P5 | Treatment (X) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 3 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 4 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 5 | 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 3 | 1 | 0 | 1 | 0 | 0 | 1 |
| 2 | 4 | 1 | 0 | 0 | 1 | 0 | 1 |
| 2 | 5 | 1 | 0 | 0 | 0 | 1 | 1 |
| 3 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | 2 | 1 | 1 | 0 | 0 | 0 | 0 |
| 3 | 3 | 1 | 0 | 1 | 0 | 0 | 0 |
| 3 | 4 | 1 | 0 | 0 | 1 | 0 | 1 |
| 3 | 5 | 1 | 0 | 0 | 0 | 1 | 1 |
| 4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 2 | 1 | 1 | 0 | 0 | 0 | 0 |
| 4 | 3 | 1 | 0 | 1 | 0 | 0 | 0 |
| 4 | 4 | 1 | 0 | 0 | 1 | 0 | 0 |
| 4 | 5 | 1 | 0 | 0 | 0 | 1 | 1 |
Note: Each row represents observations for a given cluster in a given period. The "Intercept" column is always 1 (baseline reference), the "Period" columns indicate the temporal period, and the "Treatment (X)" column indicates whether the cluster has received the intervention (1) or remains under control (0).
In this illustration, Cluster 1 starts intervention at period2 (so X goes from 0 in period1 to 1 thereafter), Cluster 4 starts at period5 (so X is 0 until period5). The period columns Period2–Period5 are 1 or 0 depending on the period. This design matrix is typically full rank (assuming not too small a number of clusters relative to parameters), allowing estimation of \(\theta\) (the treatment effect) and each \(\gamma_{j}\) (time effects) separately. It highlights an important feature: collinearity can be a concern if one attempted to include both period effects and a separate term for “time since intervention” that is strongly correlated with period in a systematic rollout. We will return to how to handle modeling of exposure time.
Adjusting for Secular Trends
In the model above, \(\gamma_j\) fixed effects (for \(j=2,\dots,J\) adjust for secular trend. An alternative is to treat time as continuous and fit e.g. a linear trend. However, stepped-wedge literature recommends using discrete period fixed effects for flexibility. Karla Hemming and colleagues emphasize that “one of the most important things when analysing a stepped wedge trial is to allow for the possibility of secular changes in outcomes over time”. If we omitted time effects, the design would inherently confound intervention effects with time effects, since later periods have more intervention and also potentially different baseline outcome rates. Thus, including time in the model is virtually mandatory.
It’s worth noting that if the number of periods is large and the cluster count modest, there could be many time parameters relative to clusters, which might reduce statistical power or precision for estimating \(\theta\). In such cases, one might consider partial pooling of time effects (e.g., treat time as random effect if one assumes a random trend) or using a parametric form, but these are advanced considerations. The usual approach is to include all period dummies and ensure the study is sized to handle that.
Accounting for Intra-Cluster Correlation
The mixed model approach with a random intercept \(u_i\) is one way to handle the intra-cluster correlation. In a linear mixed model, the variance of \(Y_{ijk}\) can be expressed as \(\text{Var}(Y_{ijk}) = \sigma^2_u + \sigma^2\) (cluster + individual variance), and the ICC = \(\sigma^2_u / (\sigma^2_u + \sigma^2)\). In generalized models (like logistic), the concept of ICC still exists (often on the latent scale or via variance partition coefficients). An alternative analytic approach is the generalized estimating equations (GEE) with robust standard errors, specifying a working correlation structure (like exchangeable correlation within clusters). GEE can provide population-averaged effect estimates and is less sensitive to distributional assumptions of random effects, but with small number of clusters one must use finite-sample corrections for standard errors (e.g., Kauermann-Carroll or Fay–Graubard adjustments).
James Hughes has suggested that it’s better to “overfit than underfit” in terms of random effects for SW-CRTs. This means including any random effect components that might reasonably account for extra correlation (for instance, random time effects by cluster if needed) so that standard errors are not underestimated. However, one must be cautious: if too many random components are included with limited clusters, estimates can become unstable. Small-sample corrections or exact/permutation tests can be employed to ensure validity. In fact, Hughes et al. (2018) proposed a permutation-based inference method yielding a closed-form estimator for the treatment effect that is robust to misspecification of both the mean model and the covariance structure ( "Robust Inference for the Stepped Wedge Design" by James P. Hughes, Patrick J. Heagerty et al. ). This method essentially does not rely on perfectly modeling the random effects or time trends and still provides valid inference for \(\theta\) by leveraging the randomized nature of the step allocation.
In summary, the analysis of a SW-CRT typically either uses (a) GLMMs with random intercepts (and possibly other random effects) or (b) GEE with robust standard errors, with both approaches adjusting for time. The GLMM provides a conditional (cluster-specific) estimate of intervention effect, whereas GEE yields a marginal (population-averaged) effect; in many scenarios of moderate to small ICC, these will be similar. The Mozambique case study (as reported in Lancet Global Health) used mixed-effects logistic regression models adjusted for clinic (as random effect) and time (step) fixed effects for the binary outcomes – a prototypical approach for SW-CRT analysis.
Sample Size and Power Considerations
Hussey and Hughes (2007) derived formulas for the variance of the intervention effect estimator in a SW-CRT. A key determinant of power is the number of clusters and the number of steps. In their formulation, with equal cluster sizes per period, the variance of the estimated effect (for a continuous outcome, under linear mixed model) has a closed form that depends on \(I\), \(J\), within- and between-cluster variances, etc.. One intuitive result is that as the number of steps increases (holding total clusters constant), precision can improve because the intervention effect is being estimated with multiple within-cluster comparisons at different times. However, diminishing returns apply beyond a certain point. Another intuitive comparison: a SW-CRT with \(I\) clusters and all clusters eventually receiving intervention can often achieve similar power as a parallel CRT with more than \(I\) clusters (because in a parallel CRT, only half the clusters would receive intervention data). Thus, SW-CRTs tend to require fewer clusters than standard parallel designs for the same power in many scenarios, which is attractive when clusters (e.g., hospitals) are expensive or limited in number.
In the Mozambique trial’s planning, they assumed an ICC of 0.05 and aimed to detect an increase in certain ANC care practices from 30% to 60% prevalence. Using stepped-wedge power calculations, they estimated that 6 clusters would be sufficient for 80% power at 5% significance. Nonetheless, they included 10 clusters to protect against loss of clusters and to increase generalizability. This exemplifies another point: SW-CRTs, like all CRTs, risk loss of entire clusters (due to dropout of a site, etc.), which can severely impact power if the number of clusters is small. Hence researchers often include a cushion of extra clusters if possible.
Analytical formulae for power in SW-CRTs have continued to evolve. Hemming et al. (2015) extended calculations to allow unequal cluster sizes and binary outcomes with logistic models, and provided a user-friendly framework for trialists. More recently, methods have been developed to calculate power when relaxing the assumption of constant treatment effect. If one anticipates, for example, that the intervention effect will not be fully realized until one period after introduction (a one-period lag), then standard power calculations (which assume instant effect) might overestimate power – because effectively one period’s worth of data per cluster is contributing less or no information on the effect. Some methodological work is addressing how to incorporate such lags into power analysis ( Current Issues in the Design and Analysis of Stepped Wedge Trials - PMC ). Conversely, if one anticipates a gradual increase in effect, one might model the effect as ramping up and then use simulation or analytical approximations to see how that influences power.
In practice, many SW-CRTs still plan under the immediate effect assumption for simplicity and then do sensitivity analyses. A practical tip from Hughes’s guidelines: “including more variance components in the power calculation reduces the possibility of an underpowered trial”. For instance, if one is unsure about potential extra sources of variability (like a possible time-by-cluster interaction), it is safer to account for it in the power calculation (even if not in primary analysis) so that the study is not underpowered if that variability exists.
Dealing with Time-Varying Treatment Effects
As discussed, one of the emerging concerns in SW-CRT analysis is the possibility of time-varying intervention effects (i.e., the effect depends on how long the cluster has been exposed to the intervention). If unaccounted for, this can bias the estimate of the “overall” effect. There are a few approaches to address this:
- Avoiding the Assumption When Unnecessary: The simplest approach is to not assume constant effect upfront – instead, model the effect with indicators for each exposure period. For example, one can extend the model to have separate parameters for being in the first period of intervention, second period of intervention, etc., for each cluster. This yields a set of effect estimates \(\theta_1, \theta_2, ..., \theta_{T-1}\) (if \(T-1\) periods of intervention possible after rollout, where \(T=J\) representing the effect in the first, second, ... period post-introduction. A global test can be done to see if these differ (\({H_0: \theta_1 = \theta_2 = \dots = \theta_{T-1}}\). If they do not significantly differ, one might decide a constant effect assumption is reasonable; if they do, it indicates a time-varying effect. However, estimating many separate \(\theta_\ell\) with limited data per \(\ell\) can be inefficient or even infeasible if \(T\) is large and clusters are few.
- Parametric Shapes for Effect Trajectory: Instead of completely distinct effects per period, researchers can impose a shape. For example, one might assume the effect ramps up linearly over a certain number of periods, or follows a logistic curve approaching a plateau. Granston (2013) proposed a two-stage approach: first estimate period-specific effects (as above), then fit a non-linear curve (like a logistic growth curve) through those estimates to model the trajectory of the intervention effect over time. Such a model could be: \(\theta(\ell) = \theta_0 [1 - \exp(-d \ell)]\) for \(\ell\) periods since introduction, meaning the effect increases with a rate \(d\) toward a maximum \(\theta_0\). This is just one example; any suitable function (even a linear \(\theta(\ell) = m \ell\) up to some point) could be used if grounded in subject-matter expectations.
- “Exposure Time” as Covariate: One can augment the dataset with a measure of exposure time. Let \(s_{ij}\) denote how many periods cluster \(i\) has been under intervention by period \(j\) (so \(s_{ij}=0\) if \(X_{ij}=0\); if the cluster started intervention at period \(q\), then for \(j \ge q\), \(s_{ij} = j - q + 1\). We could then include \(f(s_{ij})\) in the model as a covariate, where \(f\) is some function (like linear: \(f(s)=s\) to allow a linear change in log-odds per period of exposure). If \(f\) is just an indicator of \(s>0\) (exposed vs not), we are back to the basic model. If \(f(s) = s\) (and \(s\) capped at some max), that would assume a linear growth of effect each period after introduction. Non-linear \(f\) can be used similarly. Kenny et al. (2022) describe such approaches and how they relate to estimating what they term the effect curve over exposure time. In their formulation, instead of a single “the treatment effect,” we think of \(\delta(s)\) as the effect after \(s\) time units of exposure, and then define summary measures like the time-averaged treatment effect (TATE) over a range of exposure times. For instance, one might report the average effect in the first year of exposure versus beyond one year.
- Lagged Intervention Indicators: A variant is to include lagged versions of the intervention indicator. For example, include \(X_{ij}\) (intervention this period) and another variable \(Z_{ij} = X_{i,j-1}\) (intervention in previous period) in the model. This would allow the effect to be partially realized: \(\theta_1\) for initial period impact, plus additional \(\theta_2\) for subsequent periods (if \(Z_{ij}\) is 1 it indicates at least second period of exposure). This is a simpler parameterization for a “delayed” effect: if \(\theta_1 < \theta_2\), it means full effect takes two periods to manifest. More lags can be added if needed for longer transitions.
Which approach to use depends on theory and data volume. If one has many periods of data post-intervention and suspects a complex pattern, a non-parametric or very flexible approach (separate indicators) might be used. If data are sparse, one might assume a particular shape or a short lag. It is important that trialists think about this at the design stage: if a substantial delay is expected, the duration of observation after the last cluster switches might need to be extended to capture the full effect, and power calculations should account for it.
Hughes et al. (2015) note that many SW-CRTs implicitly assume instantaneous effects in design, which could lead to underpowering if there is actually a delay. They encourage investigators to consider possible “time-on-treatment” effects in both design and analysis. The use of an “exposure time indicator model” (assigning a different effect for every exposure time) is one recommendation when evidence suggests the effect might not be immediate. However, they also acknowledge it’s an open question how often this is a serious issue in practice – ongoing efforts (such as the collection of SW-CRT datasets by Hughes and collaborators in 2023) aim to empirically assess how frequently intervention effects ramp up over time in real trials.
In the case study presented below, we will see that the intervention’s effect was observed to be immediate and maintained at a high level. Thus, a simple constant effect model was adequate there. But as SW-CRTs expand to different interventions (e.g., behavioral interventions, complex multi-component programs that might slowly increase in fidelity), analysts should be prepared to check the constant effect assumption and employ more flexible models if needed.
Emerging Methods and Other Considerations
The stepped-wedge design has spurred a rich methodological research agenda. In addition to time-varying effects and robust small-sample inference, researchers are exploring:
- Design Extensions: Variants like incomplete stepped wedges (not all clusters get intervention by end, usually for ethical or necessity reasons), multiple interventions stepped-wedge (factorial or multiple sequential interventions), and continuous recruitment vs closed cohorts within clusters. Each of these brings twists to analysis; for example, closed cohort designs (following the same individuals over time) introduce correlation over time within individuals that must be modeled in addition to cluster effects.
- Analysis of Period Effects: Since SW-CRTs inherently require modeling time, some recent works have examined how misspecification of time trends affects bias or power. If an unmodeled non-linear trend exists, it could bias \(\theta\). Ensuring adequate degrees of freedom for time and possibly borrowing external trend data are areas of development.
- Software and Tools: The design’s complexity has led to specialized tools (e.g., the steppedwedge package in R or Stata routines) that help in power calculations and analysis. These often implement the formulas from Hussey & Hughes (2007) and extensions by Hemming et al., Kenny et al., etc.
- Sensitivity Analyses: Because SW-CRTs often rely on some assumptions (like no interference between clusters, properly modeled time trends, etc.), sensitivity analyses are recommended. For example, one can re-analyze assuming a time trend shape or excluding data from the first period after intervention (if one worries about transitional instability) to see if conclusions change. In the Mozambique trial’s supplementary analysis, they conducted a sensitivity analysis accounting for repeated ANC visits by the same women (a subset where women had unique IDs) to ensure that ignoring within-woman correlation did not bias results. Similarly, sensitivity to different correlation structures or including a cluster-period random effect (to allow some extra variance) can be checked.
In summary, the statistical foundation of SW-CRTs is well-established, but ongoing research continues to refine best practices. The analysis must account for clustered measurements and time trends, and should not naively assume a simple constant effect if the nature of the intervention suggests a more complex impact trajectory. Careful planning of sample size must consider all these factors to ensure a robust and ethical trial.
Results: Mozambique ANC Trial Case Study
To concretize the concepts discussed, we present the results of a stepped-wedge cluster randomized trial conducted in Mozambique that evaluated a health systems intervention in antenatal care (ANC). This trial serves as a prime example of how an SW-CRT is implemented and analyzed in a real-world global health context. We draw on the trial protocol, the published primary results in The Lancet Global Health, and supplementary materials.
Trial Design and Intervention
The Mozambique trial (2014–2016) tested an intervention aimed at improving the quality of routine antenatal care visits by ensuring consistent availability of key medical supplies. The intervention had four components:
- Kits with medical supplies: Pre-packaged kits (often referred to as “Kit A” and “Kit B” in project documents) containing essential medications and materials for ANC (for example, iron supplements, deworming tablets, dipsticks for urine protein, etc.). These kits were designed to eliminate stockouts at the point of care.
- Storage cupboard: A dedicated cupboard was provided to each clinic to securely store the kits, improving organization and accessibility of supplies.
- Tracking sheet: A monitoring tool was introduced for clinic staff to log kit usage and stock levels, enhancing supply chain transparency.
- One-day training session: Health providers (nurses and midwives) at each clinic received training on the intervention’s use, including proper ANC protocols according to updated guidelines and how to use the kits and tracking system.
The trial was set in 10 primary health center clinics across three regions of Mozambique. These clinics were selected by the Ministry of Health for participation due to their high volume of ANC patients and strategic importance. All pregnant women attending ANC in these clinics during the study period were eligible to receive the intervention once it was rolled out; there was no individual-level exclusion, making this a highly pragmatic trial embedded in routine care.
The stepped-wedge design was implemented as follows: after an initial two-month baseline period where no clinics had the intervention, one clinic was randomly selected to initiate the intervention every two months (the step interval was two months). Thus, at month 3, the first clinic began the intervention; at month 5, a second clinic started; at month 7, a third; and so on, until by the end of the 22-month study, all 10 clinics were receiving the intervention. The order in which clinics started the intervention was determined randomly in advance, ensuring a random sequential rollout. Each time a new clinic launched the intervention, outcome data from that point were counted as “intervention” data for that clinic. Clinics still waiting served as controls (providing baseline data concurrently). By design, no clinic ever stopped the intervention once started, and no clinic remained in the control state for the entire study – a complete stepped wedge.
The rationale for using the stepped-wedge design was explicitly detailed by the investigators: given the formative evidence that the intervention (supply kits) would likely benefit ANC quality, it was deemed unethical and politically untenable to provide the kits to some clinics and not others indefinitely. Moreover, due to logistical and financial constraints, the Ministry of Health could not roll out the intervention in all 10 clinics simultaneously. The stepped-wedge design thus allowed a phased implementation that aligned with resource availability, while still enabling an unbiased evaluation by randomizing the sequence of rollout. The Ministry of Health was a key partner, selecting the clinics and actively participating in the rollout and monitoring (moza.lancet.paper.pdf), which speaks to the design’s acceptance and feasibility in a policy context.
Outcomes and Data Collection
Three primary outcomes were defined, all measured at the individual patient level during ANC visits (moza.lancet.paper.pdf):
- Proportion of women screened for anaemia at the first ANC visit – i.e., was a hemoglobin test done or at least a finger-prick test for anemia recorded.
- Proportion of women screened for proteinuria at the first ANC visit – typically via a urine dipstick test for protein.
- Proportion of women who received mebendazole (a deworming treatment) during the first ANC visit (assuming they were in the appropriate gestational age window as per guidelines).
These reflect core components of evidence-based ANC (screening for anemia and preeclampsia, and deworming to prevent parasitic infections). In essence, they are indicators of whether the clinic had and used the necessary supplies (ironically, all of them require supplies that were often lacking: hemoglobin reagents or devices, urine dipsticks, and deworming tablets). Secondary outcomes included similar indicators for follow-up ANC visits (2nd, 3rd visits etc.) and measures of provider attitude, but here we focus on the primary outcomes for brevity.
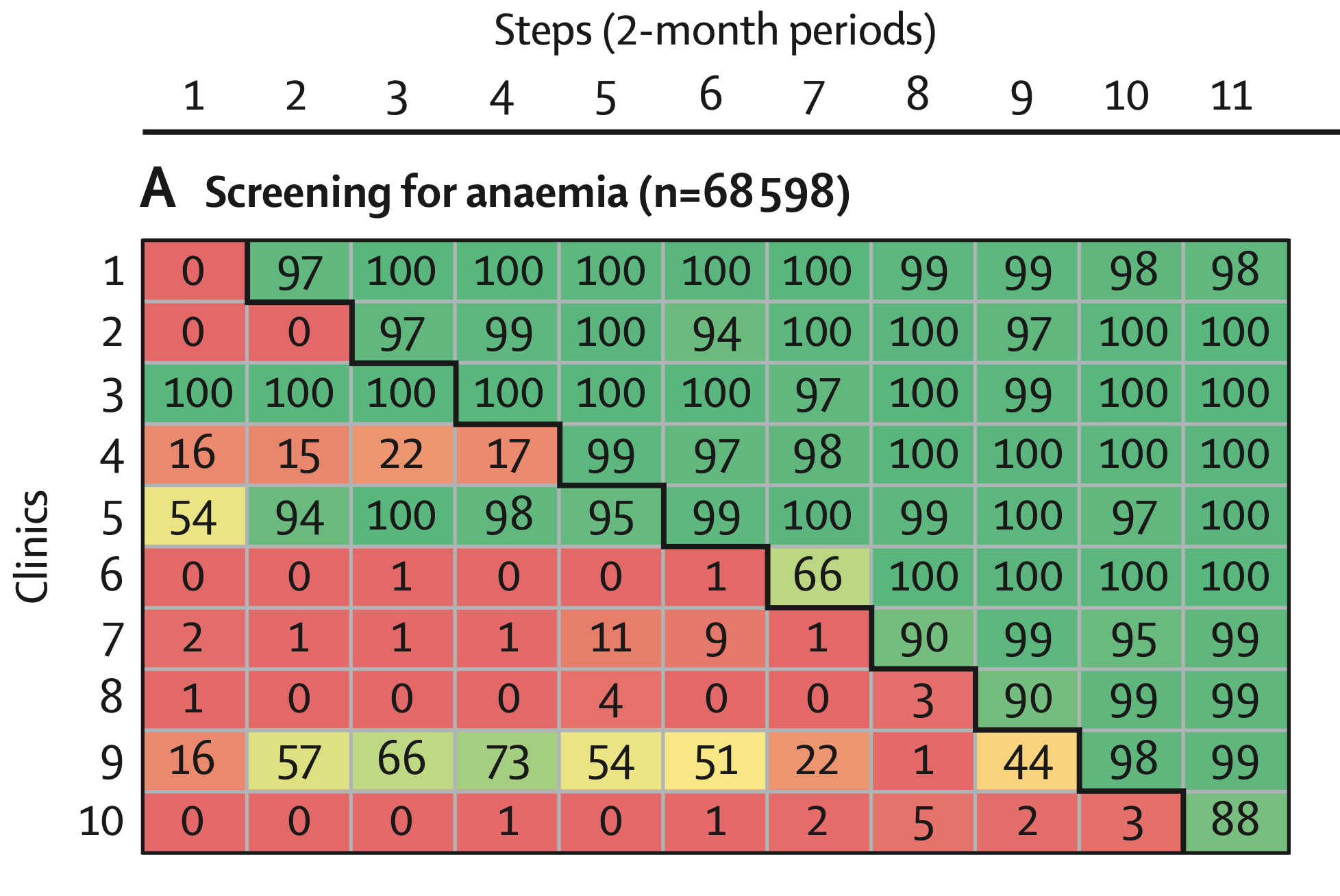
Data were collected through routine clinic logbooks that nurses and midwives fill out during ANC visits. These logbooks were adapted to ensure the relevant data points (tests done, medications given) were recorded consistently. Because the trial was conducted under routine conditions, the data capture approach leveraged existing record-keeping practices, with some enhancements for completeness. The study team also instituted data quality checks and an electronic database was created from the logbook entries. Over the entire study, a very large sample was accumulated: over 218,000 ANC visits were recorded, including 68,598 first visits and 149,679 follow-up visits. These numbers illustrate the advantage of a pragmatic trial design – by using routine data and including all patients, the study achieved a sample size that would be nearly impossible in a traditional individually randomized trial.
Analysis and Statistical Methods Used
The analysis, as reported, was based on an intention-to-treat principle at the cluster level (meaning each clinic’s data were analyzed according to the scheduled rollout, regardless of any minor deviations). The primary analysis used mixed-effects logistic regression for each binary outcome, with fixed effects for trial period (step) and a random intercept for clinic. This effectively controlled for secular trends and clinic-level clustering, respectively. The treatment effect was modeled as a fixed effect indicating whether the clinic was in the intervention phase or not for that observation. To account for potential correlation of outcomes from repeated visits by the same woman (especially relevant for follow-up visit outcomes), a sensitivity analysis was performed including a random effect for individual in the subset of data where women could be linked across visits. The main results were found to be robust, changing little with that adjustment.
Importantly, they report using a 99% confidence interval and p<0.0001 for significance – this is because the stepped-wedge design often calls for adjustment of the significance level if multiple looks or because of the correlated nature of data; however, the details suggest they may have used 99% CI due to the large sample (or possibly a typo in reporting since p<0.0001 already indicates strong significance). The results were so overwhelmingly positive that significance was not borderline in any case.
Key Findings
The intervention had a dramatic impact on the quality of ANC services delivered. Here we summarize the main outcomes, comparing the baseline (control) period to the intervention period for first ANC visits:
- Anaemia screening: In control periods, only 14.6% of women at first visits were screened for anemia (5,519 out of 37,826). In intervention periods, 97.7% were screened (30,057 out of 30,772). This difference translates to an adjusted odds ratio (OR) of about 832 (99% CI 667–1039; p<0.0001). In other words, women were hundreds of times more likely to be screened for anemia when the clinic had the supply kit intervention. The near-universal screening in intervention periods indicates the removal of supply bottlenecks.
- Proteinuria screening: In control periods, 9.9% were screened for proteinuria (3,739 of 37,826). In intervention, 97.1% were screened (29,874 of 30,772). The adjusted OR here was even larger, ~1875 (99% CI 1448–2429; p<0.0001). Again, the screening went from virtually 1 in 10 women to almost every woman, a remarkable improvement.
- Mebendazole (deworming): In control periods, 51.4% received mebendazole (17,926 of 34,842 eligible). In intervention, 88.2% received it (24,960 of 28,294). The adjusted OR was 1.88 (99% CI 1.70–2.09; p<0.0001). Unlike the tests above, the baseline here was already about half of women getting deworming, and it increased to nearly 90%. So the effect, while highly significant, is more modest in OR terms (reflecting a big improvement but not from 0 to 97%, rather from ~50% to ~88%).
It’s worth noting how massive those odds ratios for the tests are – such large ORs are unusual in intervention studies, but here they reflect that the control group performance was extremely low due to stockouts, and the intervention effectively ensured supplies such that the service could be provided to essentially everyone. The effect was immediate and sustained over time; in fact, the Lancet paper notes explicitly that the effect did not wane: once a clinic got the kits, performance jumped and stayed high. They also mention there was negligible heterogeneity between sites in these effects, meaning all clinics responded similarly to the intervention. This is an encouraging finding for scalability—every site, whether urban or rural, large or small, showed the improvement, suggesting context did not mediate the effectiveness strongly.
Secondary analyses showed improvements in follow-up visit indicators as well (e.g., women returning for later visits also benefited from tests and treatments, though calculating denominators is trickier for follow-ups). Additionally, a composite outcome and providers’ attitudes were evaluated, all suggesting the intervention package was successful in embedding a new standard of care. No serious negative effects were reported, and since the intervention was largely about supply provision, no direct patient safety concerns were noted (aside from ensuring mebendazole is given only in second trimester, which was standard practice).
Interpretation
This trial provided robust evidence that a health systems intervention addressing supply-chain failures can greatly enhance the delivery of evidence-based antenatal care in a low-resource setting. The immediate increase in screening rates suggests that the limiting factor was indeed the availability of supplies (rather than, say, unwillingness of providers). With supplies at hand (and a bit of training), nurses and midwives almost universally carried out the indicated tests and treatments. The fact that this was achieved in the context of routine care is important: it demonstrates effectiveness in the real world, not just efficacy under ideal conditions.
From a methodological perspective, the SW-CRT design was integral to the success of this study. It allowed the investigators to use all clinics as their own controls initially, improving statistical power to detect changes. Indeed, if this had been a parallel cluster trial with 5 clinics in intervention vs 5 in control, it’s possible that random baseline differences or secular trends could have clouded the results. Instead, the stepped wedge controlled for baseline differences (each clinic’s starting level was its own control) and for time trends. In reality, a large secular trend was unlikely (the changes were so huge), but if there had been any gradual improvement in ANC practices nationally during 2014–2016, the analysis would account for it with the time effects. The results clearly attribute the improvements to the kit intervention and not to other concurrent changes, because no such changes produced anything near a comparable uptick during the control phases.
One might ask: did the assumption of a constant immediate effect hold true here? The data indicate yes – the improvement was immediate (within the first measurement interval after introduction, screening rates jumped to ~97%). There was no sign of a gradual uptake; compliance was essentially instant. This likely reflects the nature of the intervention (giving supplies is a one-time change that immediately enables services). If this were a different intervention, say a training without supplies, one might have seen slower behavior change. So in this trial, the classic analysis assumption was appropriate and did not mislead. If anything, one could argue that after near 100% screening was achieved, there was a ceiling effect – you can’t go above 100%, so there’s no room for a time-varying increase. Could there have been a decrease over time? Possibly if kits were used less diligently as novelty wore off, but the sustained high coverage suggests that did not occur in the timeframe observed.
It’s also notable that because all clinics eventually got the intervention, the Ministry of Health was invested in the process throughout – an official from the Ministry was “actively involved in every step of the trial” and nurses were supervised by the Ministry as part of routine monitoring (moza.lancet.paper.pdf) (moza.lancet.paper.pdf). This illustrates how SW-CRTs can be structured as true implementation partnerships, where the research is embedded in the program rollout. The trial’s pragmatic nature (no extra research staff delivering care, use of routine data, etc.) means the results have high external validity to the context of Mozambique’s public clinics. It’s reasonable to expect that if the Ministry scales this intervention to other clinics, similar results could be obtained, since the trial conditions were essentially normal operating conditions plus kits.
The results from this trial were published in a high-impact journal and disseminated to stakeholders. As indicated in the Lancet paper’s discussion, this evidence supports broader health system decisions: for example, it provides justification for investing in improved supply chain mechanisms for maternal health, and evidence for international donors or government to prioritize ensuring commodities availability in primary care. It also contributes to the scientific literature on strategies to improve quality of care in ANC, complementing other trials in different countries.
The Mozambique ANC trial stands as a compelling case study of a SW-CRT that achieved both scientific rigor and practical impact. In the next section, we will step back to discuss the broader role of SW-CRTs in implementation science and global health, incorporating lessons from this case and others. We will then provide a section targeted at health policy makers to translate these findings into actionable insights.
Discussion
The stepped-wedge cluster randomized trial design has proven to be a valuable tool for researchers and policymakers aiming to test interventions within health systems. This discussion synthesizes the methodological considerations and case study findings, and highlights the implications for future research and practice.
Strengths of the SW-CRT Design
The Mozambique trial exemplifies several key strengths of SW-CRTs in clinical and public health research:
- Ethical Acceptability and Stakeholder Buy-in: Because all clusters eventually received the intervention, stakeholders (in this case, the Mozambique Ministry of Health and participating clinics) were amenable to the trial. No clinic felt “deprived” relative to others, which can be a major issue in parallel cluster trials when an intervention is desired by all. This likely facilitated the successful implementation – clinics were willing to delay intervention knowing it was coming and that the order was randomized (hence fair).
- Control of Secular Trends: Any improvements or changes in ANC practices due to external factors (e.g., national policy changes, seasonal variations) were controlled by the design and analysis. If, for instance, a new ANC guideline was issued nationally during the study, its influence would have affected all clinics and thus been absorbed by the period effects, not confounded with the kit intervention effect. This is a distinct advantage over simple pre-post evaluations or non-randomized rollouts, which often cannot separate intervention impact from temporal trends (The stepped wedge trial design: a systematic review | BMC Medical Research Methodology | Full Text).
- Efficient Use of Clusters: Each clinic provided data under both control and intervention conditions, increasing the efficiency of effect estimation. The variance of the effect estimate is reduced when within-cluster comparisons over time are used (especially when baseline levels vary widely between clusters). In our case study, some clinics might have started with higher screening rates than others, but each clinic’s jump (from its own baseline) contributed to the overall estimate, rather than relying solely on between-clinic differences.
- Pragmatism and External Validity: By embedding the trial in routine service delivery, the results are immediately relevant for scale-up. In many SW-CRTs, including the Mozambique trial, there were no strict exclusion criteria or heavy additional research procedures – this pragmatic approach yields findings that generalize to real practice settings. For example, the fact that data came from normal clinic logs (with some quality checks) means that the measured effect is what one might expect when implementing the intervention in the routine health information system context.
Challenges and Limitations
Despite its strengths, the SW-CRT has inherent challenges:
- Complexity of Implementation: Coordinating a staggered rollout requires careful planning. The Mozambique trial had to deliver new supplies and training to a different clinic every two months in a randomized order. This demanded logistics management and communication to ensure each step happened on schedule. Any delays could potentially affect the design (e.g., if a clinic didn’t start on time, it complicates analysis – although one can adjust actual start times in analysis if needed).
- Longer Study Duration: The design extended over 22 months. If the goal was to get results faster, a parallel design could have finished sooner (albeit with fewer data points). For outcomes where rapid results are needed (e.g., during an epidemic), a stepped wedge might be too slow, especially if each step spans months. In implementation research, however, the timeline often matches programmatic rollouts, so this is usually acceptable.
- Analysis Assumptions: The standard analysis assumes no interference between clusters (one cluster’s outcomes are not affected by another cluster’s intervention status) and no time-varying effect unless modeled. In the case study, interference was minimal because clinics and their patient populations are separate. However, in other contexts, one might worry about information spreading (a clinic seeing a neighbor implement might start copying the practices – “contamination”). In such cases, additional measures (like geographic separation or including all clusters eventually to minimize lasting differences) are important. The assumption of immediate effect was reasonable for supply availability, but for other interventions (e.g., training-based quality improvement), one should be cautious and perhaps plan for a gradual effect model or measure adherence over time.
- Cluster Size and Composition Changes: In long trials, the population in each cluster can change. For example, if a clinic’s catchment area grows or shrinks, or if the criteria for attending ANC change over time, this might affect outcomes. Stepped wedge analyses typically assume stability in cluster-level characteristics aside from the intervention. Investigators should monitor any notable changes (like staff turnover, patient volume shifts) that might need to be adjusted for or mentioned as limitations. In the Mozambique trial, they reported the number of ANC visits per clinic in 2011 was used to plan sample size, and the actual number observed was very large, suggesting that volume stayed high (or increased) uniformly.
- Loss of Clusters: Fortunately, in the case study, all 10 clinics completed the study. But if one or two had dropped out (e.g., a clinic closed or stopped data reporting), it would have created an imbalance in the design (not all sequences complete). SW-CRTs are somewhat robust to missing some data (since other clusters still provide comparisons), but loss of entire clusters is problematic. It reduces power and can bias if the loss is related to the intervention (e.g., if a clinic that had a problem with the intervention withdrew).
Generalizability and Use in Global Health
The Mozambique trial’s success raises the question: can stepped-wedge trials be similarly useful in other global health contexts? The answer from recent literature is “yes, increasingly so.” SW-CRTs have been employed to evaluate interventions like:
- Introduction of new treatment protocols in hospitals,
- Community health worker program rollouts,
- Health informatics tools (like electronic medical records) phased introduction,
- Policy interventions such as user fee removal in clinics,
- Behavioral interventions like handwashing campaigns where villages get the program in sequence.
In low- and middle-income countries (LMICs), in particular, the stepped-wedge design aligns well with the reality of phased program implementation. Often, a government or NGO plans to scale up an intervention gradually (due to resource constraints). Embedding a randomized evaluation in that process yields high-quality evidence without altering the overall plan much. It also helps ensure that the results are applicable to the actual scale-up context (since the evaluation literally took place during scale-up).
A growing number of SW-CRTs in LMICs is evident in the literature. For instance, some trials have looked at vaccination program changes, new maternal health interventions, HIV service delivery changes, etc., using stepped wedges. Implementation science researchers favor this design to rigorously test improvements in service delivery, because it overcomes the usual ethical barrier of withholding services: every community or clinic gets the improvement eventually, which can be easier to justify to authorities and communities.
However, one must ensure that the local stakeholders understand the design. There can be misconceptions – e.g., a community might wonder why they are chosen to receive the intervention later. Clear communication that order is randomized and not due to favoritism is important (the fairness argument). Also, support must be given to those clusters waiting, to maintain engagement during their control phase.
Insights from the Case Study
The Mozambique ANC trial underscores how a SW-CRT can directly inform policy. The intervention was relatively simple in concept (provide supplies and minimal training), yet the trial provided hard numbers on its impact. Post-trial, the Ministry of Health could decide to adopt this kit-based supply chain model more broadly. In fact, the involvement of the Ministry throughout means there was immediate ownership of results. This is a hallmark of good implementation research – when the implementers are partners in the trial, they trust the findings and are more likely to act on them.
It’s also a good example of using routine data. There was no expensive survey or data capture system set up just for the trial; it used existing clinic records. This both saved cost and proved a point: routine health information systems, if leveraged and improved slightly (with data quality monitoring), can be used for rigorous evaluation. It bridges the gap between research and practice: the data that managers see (logbooks, service stats) were directly used to produce the evidence, making it relatable and convincing to them.
From a statistical perspective, the case study also provides an example of a scenario where the design assumptions held and the model was relatively straightforward (no need for complex time-varying modeling). But not all interventions will behave so cleanly. In many other SW-CRTs, results might show a more gradual uptick or perhaps even some drop-off. For instance, consider an intervention providing mentorship to health workers: performance might improve slowly as confidence builds, and maybe slip if mentors leave. A constant-effect model might in that case average over those fluctuations. If the Mozambique trial had found something like 60% screening at first and 97% only after a year, it would have indicated a time-varying effect requiring further investigation (was it a delayed supply shipment issue? a learning curve?). That would complicate interpretation (e.g., do we need to plan for an adaptation period?). Thus, while our case is straightforward, researchers should always inspect their data for signs that the intervention effect is evolving over time. Graphical checks (plotting outcome rates by time for early vs late starters) can be informative even before formal modeling.
Another discussion point is whether any negative consequences occurred due to the intervention or design. The Lancet paper doesn’t report significant negatives, but one might think: Did focusing on these ANC components detract from other care aspects? Possibly not, since they were all part of standard ANC that should happen. It appears the primary limitation was simply that supplies were absent before. So providing them mostly yielded benefit. For a complex intervention, one should check for unintended effects (did something else suffer while this improved?). Stepped-wedge designs allow some detection of such effects if measured, and the longitudinal nature might catch trends like that.
Lastly, the success of the intervention begs the question of sustainability: after the study, were kits maintained? Did the Ministry institutionalize this system? The trial per se can’t guarantee long-term continuation, but it gives the evidence needed to justify it. Sustainability is beyond the trial’s scope but critical for real impact. In an academic thesis, one might not have that information, but it’s worth mentioning that SW-CRTs are often part of a continuous quality improvement process. They test an idea; if it works, the system must then continue it, ideally shifting from trial mode to full program mode. The stepped-wedge design, by virtue of having scaled up by trial end, leaves behind an already-implemented program in all clusters, which is a head start on sustainability (unlike a parallel trial where control sites might need new investment after the trial to catch up).
Future Directions
Methodologically, the field of SW-CRTs is evolving. We expect to see:
- More guidance on when to choose stepped wedge vs alternatives (some authors like Taljaard and Hemming have written decision frameworks).
- Extensions to analyze multiple outcomes or combine SW-CRT with other designs (like stepped wedge within a factorial design, etc.).
- Greater use of simulations at design stage to assess robustness of analysis plans (especially with time-varying effect possibilities).
- Increased use of SW-CRT in non-health fields as well (education, social programs) where phased rollouts are common.
- Data sharing and aggregation of SW-CRT results (as the 2023 dataset project by Hughes et al. indicates), which will enable meta-analyses and understanding how treatment effect patterns might generalize across contexts.
For the specific content area of maternal health, this trial adds to evidence that systemic fixes (like ensuring supplies) can yield as much improvement as direct clinical interventions. The SW design could be used to test other system improvements, such as new referral systems for obstetric emergencies, or introduction of digital health tools in maternity care, etc., in a phased way.
In implementation science, SW-CRTs represent a convergence of research and practice – they allow the simultaneous achievement of program rollout and impact evaluation. The discussion in the literature emphasizes being cautious: just because something can be done in a stepped wedge doesn’t mean it always should be. For example, if one truly has equipoise (uncertainty about whether an intervention helps or harms), a parallel trial might be more appropriate to allow a concurrent control group indefinitely. Stepped wedge often presumes an expectation of benefit and a desire to treat all eventually. If there is genuine uncertainty and a possibility of harm, giving it to all eventually could be unethical (if it turned out harmful, then a stepped wedge would have harmed everyone by the end). Thus, context matters. In Mozambique, the intervention was low-risk (just providing standard medicines); worst case, it would have no effect, not harm, so giving it to all was ethically fine. In other cases, one should still apply equipoise principles in deciding design.
Limitations in This Thesis
As a note, this thesis relied on published data and did not involve new statistical analysis of the raw data from the Mozambique trial. The interpretations are based on reported results. The methodological review is broad but not exhaustive; the field is vast, and certain technical aspects (e.g., derivation of variance formulas, handling of time-varying cluster characteristics, etc.) were only briefly touched upon. Nonetheless, the aim was to cover the critical aspects relevant to understanding and conducting SW-CRTs at a high level.
Policy Recommendations (Summary for Health Policy Makers)
For readers in ministries of health or other decision-making positions, this section provides a non-technical summary of why the stepped-wedge cluster randomized trial design is a useful approach and what insights were gained from the Mozambique example. It is intended to highlight practical implications for policy and implementation.
Why use stepped-wedge trials for health policies?Health policy makers often face decisions about rolling out new programs or interventions. A stepped-wedge trial allows you to evaluate an intervention while implementing it incrementally. Instead of implementing everywhere at once (with no comparison) or holding back some areas entirely (which may be unpopular or unfair), a stepped-wedge approach means you implement in phases, in a randomized order. This provides built-in comparisons over time: areas that have the intervention can be compared to those that are about to get it. Because the order is random, the comparison is fair and scientifically valid. Crucially, by the end of the study, all areas have received the new program, which is often important if the program is expected to be beneficial.
How does this support evidence-based policy?Stepped-wedge trials give robust evidence on an intervention’s impact under real-world conditions. For example, in Mozambique’s antenatal care trial, policy makers wanted to improve clinic practices by ensuring medical supplies were available. They could have just rolled out kits to all clinics at once. But by doing a phased rollout with a rigorous evaluation, they obtained clear evidence of how much the kits improved care (in this case, dramatically so). This evidence was far more convincing than anecdotal reports. It was quantitative and statistically analyzed, showing that the improvements were attributable to the intervention, not to other factors. With this information, health officials can justify scaling up the intervention to other regions, securing funding (since they can demonstrate results), and designing future programs. Essentially, it turns a rollout into a learning opportunity – you don’t just implement, you implement and learn.
Practical implications from the Mozambique case:
- Tangible Benefits: The trial showed that providing supply kits raised the quality of antenatal care substantially – nearly every pregnant woman received critical tests and treatments when kits were in use, versus very few before. For a policy maker, this quantifies the benefit: you can expect, say, a 80+ percentage-point increase in certain care indicators by adopting this supply strategy. Such numbers are powerful for setting targets and expectations.
- Scalability: All clinics in the trial could implement the intervention as part of their routine work. This suggests the intervention is feasible to scale. If only one fancy hospital managed to improve, one might worry about expansion; but here, diverse clinics (urban, rural) all succeeded. This implies that a national or provincial rollout could achieve similar results broadly.
- Resource Allocation: The stepped-wedge trial results can inform resource planning. In Mozambique, knowing that kit provision works means resources should be allocated to continue providing those kits and perhaps extend them to more clinics. The trial also provided data on how many additional tests and treatments were done (for example, thousands more anemia tests were conducted). A planner can use that to estimate supply needs for expansion.
- Policy Integration: Because the Ministry was involved and the intervention aligned with existing guidelines (it was basically enabling what policy already said should happen), the results reinforce current policy (e.g., that every ANC attendee should be tested for anemia and proteinuria) and show how to achieve it. If there were any policy adjustments needed (perhaps updating supply chain protocols), they could be informed by trial observations.
- No Disruption of Services: One big concern for health officials when doing research is: will it disrupt services or deny care? In a stepped-wedge trial, services are not denied – they continue as usual, and then change to the improved service at a scheduled time. The Mozambique trial explicitly was carried out “under routine conditions”, meaning clinics operated normally, just with better supplies after a certain date. Patients were not turned away; in fact, more patients got what they needed. For policy makers, this is reassurance that one can evaluate without negatively affecting patient care. It’s a win-win: rigorous evaluation and service improvement together.
- Capacity Building: Doing the trial built local capacity. Clinic staff were trained, officials engaged in monitoring, data was collected and analyzed. By the end of it, those capacities (supply management, data use) are strengthened. For instance, clinic staff got used to using tracking sheets and checking supplies – practices that can continue beyond the trial. So, implementing an intervention via a stepped wedge can also strengthen the health system components around that intervention.
When to consider a stepped-wedge trial:If you have an intervention that you believe is beneficial (maybe based on earlier pilots or evidence from elsewhere) and you plan to roll it out widely, consider collaborating with researchers to do it as a stepped-wedge trial. This is especially useful if:
- You cannot roll out everywhere at once (common due to budget/staff constraints).
- You want solid evidence of impact in your context.
- You need to convince funders or stakeholders with data.
- Ethically, you feel everyone should get the intervention eventually, so a standard trial that withholds it from some permanently is not acceptable.
- There is a possibility of a time trend during implementation (like a gradual improvement happening anyway) that you want to account for.
Policy decisions supported by SW-CRT evidence:Results from stepped-wedge trials can directly inform policies such as:
- Scaling up a program (e.g., making the kit supply system national policy).
- Modifying guidelines (if, say, the intervention revealed that certain practices should be done differently).
- Resource allocation (demonstrating cost-effectiveness or at least quantifying benefits to weigh against costs).
- Deciding between interventions (if one could do a head-to-head trial with stepped wedge for multiple strategies, though that’s complex).
- Strengthening health information systems (since using routine data was key, one might invest in better data systems as part of the legacy of the trial).
In Mozambique’s case, the evidence suggested that a relatively low-cost intervention (kits and training) had an enormous effect. A policy maker could take that to argue for funding from the government or donors to maintain the kit program. They could also integrate this approach into the national supply chain reforms.
Final takeaway for decision-makers:Stepped-wedge trials provide a pragmatic way to “test as you scale.” They turn the usual challenge of phased implementation into an opportunity for learning. By the end of the process, you have both a fully implemented intervention (in all clusters) and robust evidence about its impact and any challenges in implementation. This reduces the gap between research and action – the research is the action. The Mozambique ANC trial’s success in improving care without disrupting services demonstrates that such trials can be done in busy public health settings and can yield actionable knowledge. For policy makers aiming to pursue evidence-based improvements, partnering with researchers on a stepped-wedge trial can de-risk decisions and provide accountability (you can show results achieved). It is an investment in knowledge that pays off in better policy and better health outcomes.
Conclusions
The stepped-wedge cluster randomized trial design represents a powerful convergence of research rigor and practical implementation. In this thesis, we traced its origins, comparing it to traditional trial designs and highlighting how it addresses certain ethical and logistical dilemmas. We discussed in depth the statistical framework that underpins SW-CRTs, emphasizing control of secular trends and management of intra-cluster correlation, as well as the critical (and sometimes problematic) assumption of constant intervention effects over time. Recent methodological advances — many driven by James Hughes and colleagues — are pushing the field to recognize and accommodate time-varying effects, ensuring that our estimates of intervention impact remain valid even when reality is more complex than our initial models.
Our examination of the Mozambique antenatal care trial provided a concrete example of a SW-CRT in action. This trial not only delivered a clear verdict on the intervention’s efficacy (massively improving ANC service delivery), but did so in partnership with a national health system, thereby directly influencing policy and practice. The intervention’s immediate and sustained success, as captured by the trial, underscores the potential of health system strengthening measures when coupled with rigorous evaluation. Moreover, it illustrates how SW-CRTs can be effectively conducted in LMIC settings, leveraging routine data and fitting within programmatic timelines.
In clinical research, SW-CRTs are especially suited to pragmatic trials – those intended to inform real-world decisions rather than just explanatory hypotheses. They excel when full randomization at individual level is infeasible or when a staggered implementation is both necessary and acceptable. We highlighted that the design is increasingly prominent in implementation science, which often deals with interventions at the health service delivery or policy level. As health systems globally strive to become learning systems, SW-CRTs offer a methodology to learn while doing, thus reducing the delay between innovation and impact.
For health policy makers, understanding the value of SW-CRTs can open doors to closer collaboration with researchers and more robust evaluation of health programs. In an era of accountability and evidence-based policy, being able to demonstrate that a new strategy works (or sometimes, that it doesn’t or needs modification) is crucial. Stepped-wedge trials provide that opportunity without denying anyone eventual access to improvements, a critical consideration in public sector ethics.
In conclusion, the stepped-wedge cluster randomized trial is a versatile and increasingly important design in the researcher’s toolkit. Its ability to handle the passage of time, incorporate pragmatic constraints, and maintain rigorous controls makes it well-suited for many of today’s complex intervention evaluations. The Mozambique case study stands as a testament to how much can be achieved by combining thoughtful design with field execution: maternal health clinics saw transformative improvements through a program evaluated by a SW-CRT, and those results now inform broader health system decisions. As we move forward, continued refinement of SW-CRT methods (e.g., addressing time-varying effects, improving small-sample corrections, integrating economic evaluations) will further strengthen confidence in its findings. We anticipate that SW-CRTs will play a key role in generating the high-quality evidence needed to improve healthcare delivery and outcomes, especially in contexts where change must happen at scale and in real time. Researchers and policy makers should thus view the stepped-wedge design not as a complicated rarity, but as a go-to option when its unique advantages align with the problem at hand.
References
- Brown CA, Lilford RJ. The stepped wedge trial design: a systematic review. BMC Med Res Methodol. 2006;6:54.
- Hussey MA, Hughes JP. Design and analysis of stepped wedge cluster randomized trials. Contemp Clin Trials. 2007;28(2):182–191.
- Hughes JP, Granston TS, Heagerty PJ. Current issues in the design and analysis of stepped wedge trials. Contemp Clin Trials. 2015;45(Pt A):55–60.
- Chavane L, et al. Implementation of evidence-based antenatal care in Mozambique: a cluster randomized controlled trial with a stepped wedge design (Study Protocol). BMC Health Serv Res. 2014;14:228.
- Betrán AP, et al. Provision of medical supply kits to improve quality of antenatal care in Mozambique: a stepped-wedge cluster randomised trial. Lancet Glob Health. 2018;6(1):e57–e65.
- Rethinking Clinical Trials (NIH Collaboratory). Grand Rounds December 1, 2023: Guidelines for Design and Analysis of Stepped-Wedge Trials – James P. Hughes, PhD. (Key points summary of presentation).
- Kenny A, Voldal E, Xia F, Heagerty PJ, Hughes JP. Analysis of stepped wedge cluster randomized trials in the presence of a time-varying treatment effect. Stat Med. 2022;41(22):4311–4339.
- Heagerty PJ, Hemming K, Hughes JP, et al. Stepped-Wedge Cluster Randomized Trials: Protocol for Dataset Collection and Analyses. University of Washington; 2023. (Unpublished protocol for methodological project).
- Hemming K, Taljaard M. When is a stepped-wedge cluster randomized trial a good study design choice? J Clin Epidemiol. 2020; (Commentary).
- Nevins EJ, et al. Systematic review of stepped-wedge cluster randomized trials 2016–2022. (Under review / forthcoming).
- Hughes JP, Heagerty PJ, Xia F, Ren Y. Robust inference for the stepped wedge design. UW Biostatistics Working Paper 424; 2018 ( "Robust Inference for the Stepped Wedge Design" by James P. Hughes, Patrick J. Heagerty et al. ). (Proposes permutation-based estimator).
- Hemming K, Haines TP, Chilton PJ, Girling AJ, Lilford RJ. The stepped wedge cluster randomised trial: rationale, design, analysis, and reporting. BMJ. 2015;350:h391. (General tutorial on SW-CRT).
Apendix
AI Development Notes:
Stepped-Wedge Cluster Randomized Trial Design in Implementation Research and Health PolicyChatGPT
Let's look into the Mozambique ANC trial, focusing on trial protocol, dataset protocol, and Lancet publication. Searching uploaded documents in 'user_files' to confirm.
I’m pulling together the Lancet paper, trial protocol, and dataset protocol. These sources will interweave with scholarly literature to frame the stepped-wedge design in biomedical research.
Searched for James Hughes stepped wedgeChatGPT
data on James Hughes' research, examining time-on-treatment effects, heterogeneity, and cohort studies, and considering advanced modeling techniques and power/sample size calculations.
Consulting the guidelines for stepped wedge trials to ensure a comprehensive understanding of design and analysis. Progressing through details to enhance trial planning.
Read rethinkingclinicaltrials.org
ChatGPT
I’m digging into the impact of exposure time on intervention outcomes, suggesting a flexible time effect model instead of the classic immediate and constant effect assumption.
Read from moza.ANCMozambiqueProtocol.pdfChatGPT
I’m noting that the trial protocol from BMC Health Services Research 2014 outlines a demonstration project with a stepped wedge design. Ten clinics will implement interventions at random intervals, evaluating primary and secondary outcomes under routine conditions and focusing on scaling up effective interventions.
Read from moza.ANCMozambiqueProtocol.pdfChatGPT
I’m noting the cluster RCT design, specifically the use of a stepped wedge for 10 clinics. Each clinic sequentially implements an intervention with outcomes measured at each time point, likely following a repeated cross-sectional approach.
Read from moza.ANCMozambiqueProtocol.pdfChatGPT
I'm confirming market events, baseline data intervals, and outcome measurement times, alongside evaluating the logistical and ethical advantages of the stepped wedge design.
I’m identifying crucial references, including the systematic review by Brown & Lilford and others, to support the stepped wedge design's ethical and logistical benefits.
Clarifying sample size, ICC value, alpha level, and power to ensure statistical robustness and protect against dropouts, with six clusters needed but oversampling to ten.
Read from moza.lancet.paper.pdfChatGPT
Examining medical supply kits' impact on ANC quality in Mozambique. Using a stepped-wedge cluster randomised trial in 10 clinics. Key outcomes include anemia and proteinuria screening rates.
Read from moza.lancet.paper.pdfChatGPT
OK, let's see. The primary outcomes measure the proportion of women screened for anemia and proteinuria, and the proportion who received mebendazole at their first ANC visit.
Read from moza.lancet.paper.pdfChatGPT
I’m analyzing the ANC visit outcomes, noticing significant immediate and sustained improvements in anemia, proteinuria screening, and mebendazole use with negligible site heterogeneity.
Read from moza.lancet.supp.pdfChatGPT
I’m thinking through the potential inclusion of follow-up outcomes like anemia and protein screening, and how these might show similar positive effects. This reinforces the analysis of follow-up visits.
Read from moza.lancet.supp.pdfChatGPT
I'm mapping out the challenges of repeated visits in the main analysis, using routine logbook data.
Read from moza.SW Datasets Protocol 08Jan24 final (1).pdfRead from moza.SW Datasets Protocol 08Jan24 final (1).pdfChatGPT
, I’m gathering info on Hemming & Taljaard's notable work. Their 2020 publication seems to be a review or guideline, possibly in Trials. It includes various guidelines and commentaries.
Searched for Hemming Taljaard 2020 stepped wedge strengths and limitationsChatGPT
I’m considering aligning citations by using 【source†L...】 in the text, ensuring a consistent academic style, and possibly listing them numerically at the end while maintaining their clickable nature.
I’m organizing the thesis: summing key points in the abstract, historic context in the intro, detailed technical methods section, and a clear conclusion with policy insights.
Searched for Brown Lilford 2006 stepped wedge trial reviewChatGPT
OK, let me see. I’m gathering info on the global health use of the stepped wedge design, first used in trials like the hepatitis vaccine in Gambia.
I’m listing key sources such as Brown & Lilford 2006, focusing on essential development references. This clarity helps avoid a cluttered, confusing explanation later on.
Read bmcmedresmethodol.biomedcentral.com
ChatGPT
Sifting through various motivations for research participation: ethical, practical, scientific, and resource constraints. The analysis spans simple isolated steps to complex random effects models.
Read more from bmcmedresmethodol.biomedcentral.com
ChatGPT
I’m piecing together early mentions and empirical examples of staged introduction in innovation, noting Cook and Campbell's conceptual discussion and the Gambia Hepatitis Study as the first empirical instance.
Read more from bmcmedresmethodol.biomedcentral.com
ChatGPT
It's interesting to see how the stepped wedge design leverages phased intervention and rollout, despite its challenges like prolonged duration and contamination risks.
Read biostats.bepress.com
ChatGPT
Hughes et al. (2018) propose robust inference, allowing consistent inference without specific model assumptions, impacting advanced statistical methods.
ChatGPT
I’m gathering info on a manuscript by Hughes et al. (2015) that addresses stepped wedge designs in CRT and implementation studies, focusing on time-on-treatment effects, treatment effect heterogeneity, and cohort studies.
Read pmc.ncbi.nlm.nih.gov
ChatGPT
Thinking through how rollout pace and timing shape treatment effects, exploring adjusted models for precise estimations.
Read more from pmc.ncbi.nlm.nih.gov
ChatGPT
I'm piecing together statistical features for the cohort design, including sample size determination and variance analysis, using Hussey & Hughes 2007 as a key reference.
Searched for Hussey 2007 stepped wedge trialsChatGPT
I'm gathering info on model (1) from Hughes 2015, likely based on Hussey & Hughes 2007. This paves the way for a possible power calculation.
ChatGPT
I'm mapping out how SW designs need fewer clusters but take longer due to sequential control. Also, considering the need for a design matrix and time effects explanation.
Read from moza.SW Datasets Protocol 08Jan24 final (1).pdfChatGPT
Breaking down the stepped wedge, I’m examining ASCII formats and periods 1-5 with clusters 1-4. This seems to be a structured pattern at play.
Read from moza.SW Datasets Protocol 08Jan24 final (1).pdfChatGPT
The dataset protocol details a classic stepped wedge schematic with 4 clusters and 5 periods, emphasizing the "instantaneous and constant assumption" and its limitations.
Searched for Kenny 2022 stepped wedge time varyingChatGPT
I'm analyzing "Analysis of stepped wedge CRTs in presence of time-varying effect" by Avi Kenny et al. The work likely appears in a major method paper in Stat Med, from around 2022.
Read pmc.ncbi.nlm.nih.gov
ChatGPT
I’m pulling together a structural model with GLM, time trends, treatment effects, and random effects. This involves examining design matrix X and considering how effect variance with exposure time could bias results.
Searched for stepped wedge power formula Hemming HusseyChatGPT
I’m emphasizing the Mozambique trial's pragmatic design, thorough data collection, and external validity, particularly in a global health context.
Read from moza.lancet.paper.pdfChatGPT
Government commitment appears to enhance uptake. The Mozambique case study showcases integration, boosting policy alignment.
Read bmj.com
ChatGPT
OK, let's consider ongoing research on whether constant treatment effects are always predictable in software analysis. This involves extensive trial data and new methods for data comparison.
I’m pulling together SW-CRT design, statistical methods, the Mozambique ANC trial, and practical applications for policy makers.
I’m piecing together an integrated citation style, pairing clickable in-text references with a detailed references section, aligning with institutional presentation preferences.
I’m compiling citations from a variety of sources, ensuring each is accurately referenced to support the claims and findings presented in the thesis.
I'm detailing the incorporation of cluster and period random effects into regression models, crucial for advanced statistical analysis in the SW-CRT design.
Wrapping up the thesis with sections like policy implications, statistical methods, and Mozambique case study. Ensuring accessibility and clarity throughout the document.
I'm thinking through how new methodologies, like Kenny et al 2022, can refine design guidance for time-varying effects, emphasizing the critical interplay between secular trends and exposure time effects.
I’m working on the thesis structure, including sections like Abstract, Introduction, Literature Review, Methods (Statistical Methods), Results (Mozambique ANC trial outcomes), Discussion, Policy Recommendations, and References, ensuring each is clearly articulated and assigned.
I'm thinking about whether to include informal sources like online summaries for a PhD thesis. Mapping out the relevance and citing where necessary, considering their expert alignment and alignment with formal works.
Searched for Kenny Voldal 2022 stepped wedge publicationChatGPT
Piecing together pivotal sources like Brown & Lilford (2006), Hussey & Hughes (2007), and Hughes et al (2015). Possibly including contemporary reviews for broader insights.