Is Causation Doomed?

Introduction

Pierre-Simon Laplace famously envisioned an “intelligence” that, knowing the exact state of every particle at one instant, could predict the entire future (and past) of the universe by applying the laws of motion (Laplace's demon - Wikipedia). This idea embodies a deterministic, Markovian worldview: the universe’s state at time t uniquely determines its state at time t+Δt via time-local differential equations. In Laplace’s classical picture, the present state is both the effect of the past and the cause of the future (Laplace's demon - Wikipedia). The question we examine is whether “all there is” — at the deepest level of physical reality — can indeed be described as one giant Markovian differential equation. We must probe the conceptual coherence of this notion and test it against modern physics. Developments in quantum theory, especially entanglement and Bell’s theorem, challenge naive forms of determinism and locality.

We are challenging the status of causation in fundamental physics:

is cause-and-effect a fundamental feature of the world or merely a convenient heuristic?

Further, alternative formulations like Feynman’s path integral recast physics in terms of probabilities and histories rather than single trajectories. We will explore how viewing laws as conditional probabilities (e.g. calculating $P(\text{Outcome B}|\text{Condition A})$) contrasts with the traditional differential equation paradigm. Finally, we speculate on possibilities beyond the Markovian paradigm – such as global constraints or retrocausal influences – and discuss what is gained or lost when moving from deterministic “laws of motion” to more generalized, probabilistic descriptions. Throughout, we aim for a philosophically informed analysis of whether Laplace’s dream of a cosmic differential equation still holds in light of contemporary physics.

Laplace’s Deterministic Vision and the Markovian Paradigm

Laplace’s vision encapsulates the idea of the universe as a closed mechanical system governed by deterministic laws. In classical mechanics, if one has a complete specification of all particle positions and momenta at a given time (the microstate), Newton’s equations (or more generally Hamilton’s equations) allow one to compute the state at any future (or past) time. This is essentially a Markovian evolution: the dynamical laws are time-local (typically first-order in time for the state vector), meaning the future depends only on the present state, not on any hidden memory of the system. The result is a single “trajectory” of the universe in state-space, fully determined by initial conditions. As Laplace put it, such an intellect would capture “in a single formula the movements of the greatest bodies and those of the tiniest atom,” with nothing left uncertain (Laplace's demon - Wikipedia). In this paradigm, the conceptual apparatus of causation is subsumed by mathematics – every state is the lawful result of the previous, so one might say the differential equation itself is the ultimate cause. The Markovian, deterministic paradigm was spectacularly successful in the 18th–19th centuries: it underlies classical celestial mechanics, which can predict planetary motions years in advance, and Maxwell’s equations, which determine electromagnetic fields evolving in time. Even statistical irreversibility (thermodynamics) did not obviously overthrow Laplace’s idea, since in principle the microstate (including molecular details) still follows reversible Newtonian laws (the apparent irreversibility arises from ignorance of details or special initial conditions). Thus, at first glance, the idea of a giant differential equation governing all might appear conceptually coherent and in line with classical physics’ triumphs.

However, even within classical physics, some nuances emerge. Chaos theory reveals that while deterministic, classical systems can be exquisitely sensitive to initial conditions, making long-term prediction effectively impossible for practical “demons.” This doesn’t break the Markovian deterministic paradigm but shows its epistemic limitations – finite beings can’t achieve Laplace’s omniscience. More fundamentally, in general relativity, the “state” of the universe is constrained by global conditions (the Einstein field equations impose constraints on a spacelike slice, and spacetime as a whole might not be globally hyperbolic in all solutions). Still, general relativity is local in time evolution (for well-posed problems) and deterministic in classical form. Thus, up through the early 20th century, one could consistently hope that the entire universe is describable by a deterministic Markovian law of evolution. The conceptual coherence of this idea rests on assuming: (a) a well-defined state of the whole universe at a given time, (b) exact laws with no indeterminism, and (c) no need for any external “meta-law” or teleological principle beyond the differential equation. Under those assumptions, the universe-as-equation concept is logically self-consistent.

Quantum Mechanics: Indeterminism and Nonlocality

The early 20th century brought quantum mechanics, which dramatically altered the Laplacean picture. Quantum mechanics introduced indeterminism at a fundamental level (at least in the standard interpretation): even complete knowledge of the quantum state (the wavefunction) does not allow certain prediction of measurement outcomes, only probabilities. In the Copenhagen view, the evolution of an isolated system’s wavefunction is deterministic and governed by Schrödinger’s equation (which is a kind of giant differential equation, linear and unitary). However, when a measurement occurs, the wavefunction appears to collapse randomly into an eigenstate, with probabilities given by Born’s rule. This collapse is not described by Schrödinger’s deterministic equation and seems to involve irreducible chance. Thus the universe cannot be described by a single, simple differential equation unless one either (i) extends the state to include the observer and apparatus (treating everything quantum mechanically) or (ii) postulates an underlying hidden determinism beneath the quantum probabilities. Option (i) leads to the Many-Worlds interpretation – arguably restoring a kind of Laplacean determinism at the level of the universal wavefunction – while option (ii) leads to hidden-variable theories (like de Broglie–Bohm pilot-wave theory) that aim to reproduce quantum statistics via unseen variables that do obey a deterministic law. Crucially, John Bell showed that any hidden-variable theory that maintains locality (no faster-than-light influence) cannot reproduce all the predictions of quantum mechanics (Bell's theorem - Wikipedia). In Bell’s words, “if [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local” (Bell's theorem - Wikipedia). Bell’s theorem and the subsequent Bell test experiments (Clauser, Aspect and others) demonstrated that no local deterministic model can account for the observed correlations of entangled particles (Bell's theorem - Wikipedia). This implies that any “giant equation” underlying quantum phenomena cannot respect both determinism and locality together.

Quantum entanglement reveals that the Markovian, time-local idea of evolution may be incomplete. In a Markovian story (especially a local one), what happens in region A at time t+Δt is determined by the state of region A (and its immediate neighbors) at time t. Yet entangled particles show correlations that cannot be explained by any story in which each particle carries its own evolving state independent of the other after they separate. Either some sort of nonlocal influence exists or the common cause of the correlation lies outside the normal space-time description. A deterministic hidden-variable theory that does reproduce quantum entanglement must be strikingly nonlocal. Indeed, the Bohmian pilot-wave theory does exactly this: it introduces a quantum wave (the pilot wave or wavefunction) that instantaneously affects distant particles’ behavior. As Bell noted, Bohm’s model has a “gross non-local structure” (John Stewart Bell), implying that the putative giant differential equation for the universe would not be Markovian in a spatially local sense – it would permit instantaneous connections across arbitrary distances (albeit structured so as not to allow controllable signaling). Such nonlocality, while compatible with the letter of Laplace’s idea (determinism), undermines the intuitive Markovian narrative of each part of the universe marching to its own local drum. Alternatively, some researchers have considered abandoning determinism but keeping locality by allowing the causal arrows to reverse or by correlating them in conspiratorial ways. For example, one proposal is superdeterminism, wherein everything – including the choices of experimenters – is predetermined and correlated from the start (John Stewart Bell). In a superdeterministic universe, the reason measurement settings and particle properties appear independent (an assumption of Bell’s argument) is because we incorrectly assume free will or statistical independence; if both experimenter and particle states were set by a common cosmic initial condition, Bell’s inequality could be violated without nonlocal communication (John Stewart Bell). This salvages a single grand deterministic equation at the expense of jettisoning any notion of independent free choice (the “free will is an illusion” scenario (John Stewart Bell)). Another route is to posit that influences can go backward in time (retrocausality), so that what we call an outcome might be influenced by future measurement settings – thereby explaining entanglement correlations without superluminal communication. Thinkers like Huw Price and physicists like John Cramer have explored such retrocausal models (John Stewart Bell). Retrocausality breaks the usual Markov condition because the future can affect the present, effectively inserting a kind of history-dependent influence (non-Markovian in time).

In summary, quantum mechanics forces us to confront non-classical features: true randomness (in standard quantum theory) and entanglement that defies locality. A “giant differential equation” describing the universe can be maintained in certain interpretations – e.g. Many-Worlds has the universal wavefunction obey Schrödinger’s equation globally, and Bohm’s theory has deterministic evolution of positions + wavefunction – but such models pay a price. Many-Worlds gives up on a single reality (splitting into branches), while Bohm gives up locality. Both still have a Markovian, time-local evolution law for the underlying state (wavefunction obeys a local differential equation in time, though in configuration space; Bohmian particles follow a guidance equation). Whether one finds these satisfactory depends on what one considers non-negotiable (realism, single outcomes, locality, etc.). If, on the other hand, one takes the observational stance of quantum theory at face value, the universe appears not to run strictly by a single reversible equation – instead it involves irreducible probabilities and perhaps events that are not determined by prior events (spontaneous radioactive decays, for example). In that case, Laplace’s notion fails: the most one can do is compute probability distributions for outcomes, not certainties. The idea of a giant Markovian equation might then be relegated to an approximation or an idealization, not the actual “operating system” of the universe.

Is Causation Fundamental? The Russellian Challenge

The question of a “giant differential equation” is deeply connected to the notion of causation. In a Laplacean universe, one might say every state is caused by the preceding state according to the law. But philosophers have long noted that fundamental physics equations themselves do not explicitly use the word “cause.” In fact, Bertrand Russell in 1913 argued that the concept of cause is not fundamental in advanced sciences: “in advanced sciences such as gravitational astronomy the word cause never occurs,” and “the reason why physics has ceased to look for causes is that, in fact, there are no such things” in the sense of fundamental cause-effect pairs (). He famously concluded that “the law of causality … is a relic of a bygone age, surviving, like the monarchy, only because it is erroneously supposed to do no harm” (). Russell observed that physics deals with functional relations and differential equations that link states at different times, but it does not label one state the “cause” and the later state the “effect” – that causal language is a heuristic overlay we humans apply. In modern times, philosopher of physics John D. Norton has echoed this view, arguing that cause and effect are not part of the fundamental ontology of physics but rather a kind of folk concept or an emergent descriptor we use in domains where interventions and asymmetries matter ((Microsoft Word - 003004.doc)). Norton’s thesis of “causation as folk science” suggests that while we can recover causal notions in special sciences (chemistry, biology, everyday events), at the level of fundamental physics we have just law-governed processes without any necessity to identify discrete causes and effects ((Microsoft Word - 003004.doc)).

If the universe is indeed fully described by a timeless set of equations (like a grand differential equation or perhaps an action principle), one might lean toward eliminativism about causation at fundamental level – meaning that the world is just governed by patterns or laws, and “cause” is a convenient summary of those patterns in certain regimes. In a fully deterministic Markovian universe, one could say the state at t1 “causes” state at t2, but this is more a trivial restatement of the fact that the evolution law holds. The real explanatory power lies in the law (equation) itself, not in an independent causal agency. Russell’s point was exactly that: when we have a precise law connecting events, invoking “cause” doesn’t add anything except perhaps intuitive gloss.

On the other hand, if fundamental physics cannot be captured by a neat time-evolution law (as quantum indeterminism might imply), does causation make a comeback, or is it further undermined? It depends. Some interpretations of quantum mechanics, like retrocausal interpretations, explicitly play with reversing cause-effect at the micro level (the effect precedes its cause). These are still fringe, but they indicate that the notion of a fixed causal order might not be sacred. Meanwhile, in practical scientific explanation, we continue to use causal reasoning (for example, in relativistic physics we talk about light cones and what events can influence others – a notion of local causality). Bell’s theorem even used a concept of “local causality” as an assumption: roughly, that events in one region are independent of distant events, given the common cause in their past light cone (John Stewart Bell). Violations of Bell’s inequality suggest that either local causality fails or some other principle (like free choice) fails, so either way our classical notion of causal order is under strain.

Some scholars propose that causation might be emergent from a deeper level that is acausal. For instance, if the universe’s fundamental description is a static four-dimensional block (as suggested by the block universe view in relativity), then what we call cause and effect might be a way of describing relationships within that block from an embedded time-bound perspective. We human observers, limited in time, see regularities and call earlier events “causes” of later ones. But in the 4D block, there is just an interrelated tapestry of events obeying the equations. If one embraces this view, then asking “what causes what?” is like asking which part of a pattern causes another part – it’s often an ill-posed question at the fundamental level. Not everyone agrees; some think cause is too useful or fundamental to discard. But even those working on quantum gravity or other frontier theories tend to focus on constraints and relations (e.g., the Wheeler-DeWitt equation in quantum gravity has no explicit time – it’s a constraint equation $H\Psi = 0$). This hints that the ultimate law might not be a time-evolution equation at all, but rather a global condition – which again doesn’t square well with a naive cause-effect narrative.

In summary, the role of causation in physical theory appears to be at most secondary. A giant Markovian differential equation, if it existed, would likely be seen by Russell and Norton as eliminating the need for a fundamental causal principle – it would be a unified explanation where each state follows from the previous by necessity, not by “influence” or “agency.” If modern physics suggests this picture is false or incomplete, it often does so in ways that further challenge simple causal intuitions (nonlocal correlations, acausal global constraints, etc.). Thus, both the strict Laplacean determinist and the quantum physicist might agree that “cause” is not an ontologically fundamental category – in the former case because everything is determined by law, in the latter because things may just happen by acausal chance or holistic constraints.

The Path Integral: Histories and Conditional Probabilities

One of the most profound reformulations of physical law in the 20th century is the path integral formulation of quantum mechanics (developed by Feynman). Instead of focusing on the state of the system at each instant evolving via a differential equation, the path integral considers all possible paths or histories between two boundary conditions. In this framework, the central object to compute is the amplitude or probability for the system to go from an initial state A to a final state B. In fact, one can say that “strictly speaking, the only question that can be asked in physics is: What fraction of states satisfying condition A also satisfy condition B?” (Path integral formulation - Wikipedia). This fraction is essentially a conditional probability $P(B|A)$ – the probability of B given A. In the path integral formalism, $P(B|A)$ is calculated by summing over (integrating) all histories (paths) that start in condition A and end in condition B, and taking the ratio with the sum over all histories starting in A (to ensure proper normalization) (Path integral formulation - Wikipedia).

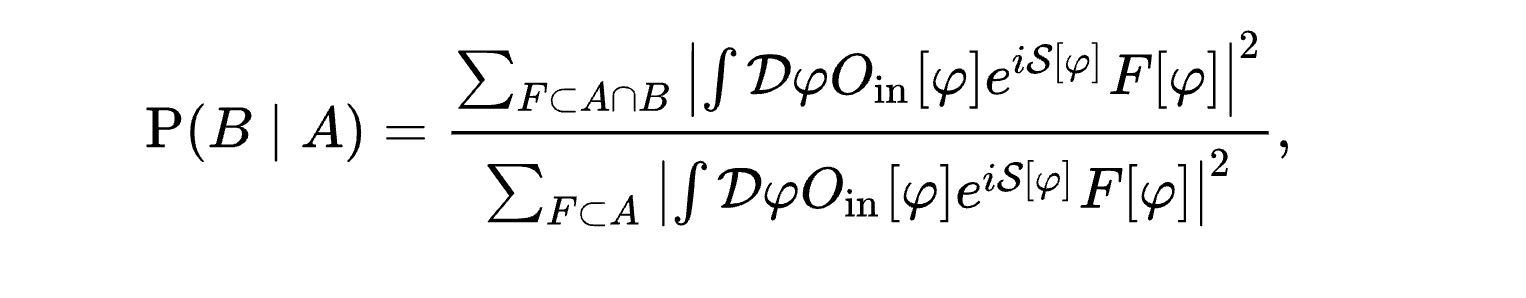
Path integral expression of the conditional probability $P(B|A)$. Physics, fundamentally, can be viewed as answering what the probability is of finding outcome B given initial condition A. The formula above shows $P(B|A)$ as a normalized ratio of two path integrals over all field configurations $\varphi$ that satisfy condition $A$ (in the denominator) and both $A$ and $B$ (in the numerator) (Path integral formulation - Wikipedia). It encapsulates the idea that dynamics is about correlations between conditions, rather than a local push-forward in time.

This perspective is a marked shift from the traditional deterministic equation of motion view. Rather than saying “Given A now, the state a moment later will be X, and then Y, and eventually B,” the path integral says “Given A at $t_0$ and B at $t_1$, the amplitude is obtained by summing over all possible ways (paths) the system could evolve between $t_0$ and $t_1$.” Importantly, the path integral formalism still contains the usual differential equations (they emerge as conditions for stationary phase in the classical limit, yielding Euler–Lagrange or Schrödinger equations). However, it emphasizes a global, probabilistic viewpoint. Markovian locality in time is somewhat obscured: one can break the path integral into segments (and indeed the composition of conditional probabilities retains a Markov property mathematically — this is related to the composition of propagators), but conceptually one often thinks of the path as a whole contributing to the outcome. This can be interpreted as the universe being “recorded” in an ensemble of histories, rather than following one single history pre-ordained by a differential equation.

The path integral also meshes well with a time-symmetric or “block time” view: since it often treats boundary conditions at both past and future, it doesn’t fundamentally distinguish cause from effect. For example, in computing a propagator $K(B,t_1; A,t_0)$, one uses contributions from all intermediate configurations. The formulation is inherently about conditional probabilities $P(B|A)$, not about time-evolution in the ordinary sense. As the Wikipedia text suggests, an extreme view is that all of physics reduces to finding $P(B|A)$ for appropriate conditions (Path integral formulation - Wikipedia). Even the entire universe’s history could be seen as the answer to “Given the state just after the Big Bang (A), what is the probability of getting some final condition B at the end of time (or at present)?” (Path integral formulation - Wikipedia). In principle, if we had the exact path integral for the universe, we’d have a giant conditional probability connecting initial and final states – an object less like a differential equation and more like a probability amplitude functional.

Does this challenge the Markovian differential equation view? In some ways, yes. It suggests that the primary reality might be a huge correlation between beginning and end, rather than a step-by-step evolution. In practice, of course, the path integral formalism is equivalent to the Schrödinger equation for quantum mechanics – one can derive one from the other – so it’s not that physics has changed, but our interpretation can change. The path integral invites a different metaphysics: one where histories are central and where the idea of a single actualized history is a derived concept (perhaps arising only in the classical limit or in consistent observation records). In a path integral or “sum-over-histories” picture, Markovianity is hidden beneath the surface. Technically, quantum propagators do satisfy composition (and thus a form of Markov property), but the need to sum over many paths to compute an outcome means the effective behavior of observed quantities can appear non-Markovian. For instance, an interference pattern arises because an electron effectively took multiple indistinguishable routes – something a classical deterministic trajectory would never do.

The path integral also resonates with certain probabilistic or information-theoretic interpretations of quantum physics. If one adopts an operational view (quantum theory as a tool for predicting measurement outcomes from preparations), then indeed what we care about is $P(\text{outcome}| \text{preparation})$. The theory doesn’t necessarily tell a story of how the outcome happens (the “mechanism” or cause); it just provides the probability. In Feynman’s formulation, one can say the mechanism is “it takes all possible paths,” which is a revolutionary description – it’s as if nature doesn’t commit to a single trajectory until somehow the measurement demands a single outcome. This idea defies the classical Markovian trajectory picture, replacing it with a stochastic spread of possibilities that only yield definite facts when observed.

From Equations to Information: Shifting Paradigms

Increasingly, some physicists and philosophers consider the possibility that the foundation of physics might be informational or probabilistic, rather than mechanical. The giant differential equation view assumes an exact, observer-independent state that evolves. But quantum mechanics, especially in some interpretations, suggests knowledge and information play a fundamental role (for example, in QBism or other epistemic interpretations, the quantum state is more about our information than a physical wave in reality). Even apart from interpretation, quantum experiments only ever give us statistical distributions of outcomes. Thus one proposal is to accept that probability is fundamental – not just as a practical tool but ontologically. If so, the laws of nature might be better expressed as rules for updating probabilities (analogous to Bayesian inference or conditional probabilities) rather than as deterministic equations of motion.

What would it mean to replace “law of motion” with “law of conditional probability”? One immediate consequence is that it acknowledges irreducible uncertainty. For instance, if the best we can do is say “From state A, outcome B occurs with probability p,” then we have embraced a stochastic worldview. This is already how one treats quantum measurement theoretically, or how one uses thermodynamics (giving probabilities for fluctuations, etc.). A fully information-theoretic physics might dispense with the idea of a single, exact history of the universe and instead describe the universe by a probability distribution over many possible histories or configurations. Some approaches like Consistent Histories in quantum theory, or the many-worlds idea (where the “measure” on branches is given by probability amplitudes), reflect this shift. In classical physics too, one can take an information view: Liouville’s equation governs the probability density in phase space rather than individual trajectories, and one can say that is just as fundamental a description as tracking one micro-trajectory.

Epistemologically, moving to a probabilistic formalism aligns physics with how we actually know and predict things – through probabilities and statistics. It also might provide a more robust framework in situations where the concept of a precise state breaks down (like near quantum gravity regimes, where spacetime itself might be indeterminate). Some researchers frame physical laws as constraints on information. For example, principles like entropy increase or uncertainty relations can be thought of as information-theoretic constraints rather than dynamics per se. The extreme view is John Wheeler’s famous aphorism “It from bit”, suggesting that at a deep level, reality might be information-based. In such a paradigm, the “giant equation” might be replaced by something like a global probability distribution or an algorithm for updating that distribution given new conditional data.

However, there are also metaphysical costs to this shift. If one abandons an actual evolving state for a cloud of probabilities, one must ask: probability of what? In a deterministic model, one could say the universe is in a particular microstate, even if we don’t know it. In a strict probabilistic interpretation (without underlying hidden variables), one might say the microstate itself is not determined until observed, only the distribution is real. This can border on anti-realism or at least a very observer-dependent reality, which is philosophically unsettling to some. It also raises the question of whether probabilities are the ontic structure of the world or just reflecting our ignorance. If ontic (as in some quantum approaches), then the universe fundamentally is a tendency or potential for events rather than concrete events – quite a departure from the clockwork image that Laplace had. Some interpretations (like objective collapse models) try to have it both ways: mostly deterministic evolution plus occasional random jumps with well-defined probabilities, effectively building stochasticity into the laws of motion themselves.

Another implication of preferring conditional probabilities is that time might be treated more symmetrically. A Markov differential equation picks out a direction (you evolve forward in time using it, although mathematically one can often invert it to go backward). But a rule for $P(B|A)$ doesn’t inherently distinguish past from future; it’s just a relation between two conditions. Indeed, the path integral formula for $P(B|A)$ is time-symmetric (the underlying action typically is time-symmetric). If the fundamental law is something like “the conditional probability of a later boundary given an earlier boundary is X,” one could equally talk about the probability of an earlier state given a later one – it would be just as well-defined (this relates to time-reversal invariance). Only when we impose additional conditions (like an initial state with low entropy, or an arrow of time condition) do we get an asymmetric sense of cause->effect. Thus, moving to a probabilistic view might actually let us incorporate the arrow of time as a separate ingredient (entropy or cosmological initial conditions) while the core laws remain time-symmetric correlations.

In practical terms, an information-theoretic formalism often uses tools like Bayesian networks or causal networks to describe systems. In classical domains, Judea Pearl’s causal networks give a way to encode causal structure as a graph with conditional probabilities on nodes. One could imagine something analogous for fundamental physics – perhaps a network of events connected by probabilistic conditional dependencies instead of a single global state evolving. Indeed, some approaches to quantum gravity (like the causal set program) represent spacetime as a network of relations, though currently those are still meant to recover a kind of local equation on average. Quantum computation and quantum information science also encourage thinking of physical processes as information-processing channels – again emphasizing inputs and outputs (conditions and outcomes) rather than a continuous mechanical evolution.

What is gained by such perspectives is a kind of flexibility and perhaps conceptual clarity about what physics actually predicts (correlations between observables). It acknowledges that, at the end of the day, our connection to the universe’s “giant equation” is indirect – we always summarize our knowledge in terms of conditional statements (“if the system is prepared in state A, then measurement B will yield result y with probability p”). By focusing on those, we avoid committing to unobservable elements (like exact trajectories or exact hidden states) that might lead to philosophical conundrums. For example, one might avoid the measurement problem by saying quantum theory doesn’t need to tell us what is, only the probabilities of experiences we will have – a view some take in Quantum Bayesianism.

What is lost or at risk, however, is the sense of reality and mechanism. A deterministic differential equation gives a satisfying feeling of mechanism – the universe has “gears” that turn in a definite way. Replacing that with abstract conditional probabilities can feel like giving up on understanding how nature does it. Some might argue that’s an illusion of understanding anyway; others feel it’s crucial. Metaphysically, a world of just $P(B|A)$ might be a world of happenings without causes, which is troubling if we insist that for something to be real it must happen somehow. The probabilistic formalism might be silently complete – not telling any deeper story because there isn’t one – or it might be silent but incomplete, meaning there is a deeper story (like hidden variables or a multiverse) but we just don’t see it. This debate is at the heart of quantum interpretations. In essence, shifting to an information paradigm often aligns with a positivistic or empiricist philosophy (focus on observable correlations, agnostic about underlying reality) as opposed to a realist philosophy (the universe is doing something definite, described by laws). Each approach has its epistemic virtues: the former never claims more than can be tested, the latter strives to describe a reality assumed to exist.

Beyond Markovian Equations: Global Constraints and Retrocausality

Even as physics has largely moved from strictly deterministic equations to probabilistic rules, it still usually assumes a Markovian (memoryless) structure in time at the fundamental level – i.e. that given the state now (whether definite or a quantum state), the future is determined (or at least its probabilities are determined). However, some speculative ideas suggest the universe’s workings might be non-Markovian or global in ways we haven’t yet recognized. One suggestion comes from the puzzle of entanglement and quantum nonlocality: perhaps the world has additional global constraints that are not captured by evolving a state forward in time, but rather relate distant events in a holistic manner. For example, one way to view violations of Bell’s inequalities is that the outcomes in spacelike separated regions are coordinated by something outside the normal forward light-cone evolution. Superdeterminism is one extreme proposal here: the “coordination” is via the initial conditions of the universe – essentially a built-in correlation from the very beginning that ties together variables that we thought were independent. This makes the evolution trivially Markovian (because initial state dictates all), but the pattern of outcomes will show what looks like conspiracies. While superdeterministic theories are deterministic and Markovian in time, they introduce a kind of ad hoc global knitting of events that many find implausible (and experimentally, tests of freedom of choice have so far upheld quantum predictions, though loopholes remain).

Another angle is the idea of two-time boundary conditions. Some physicists (and science-fiction writers alike) have entertained the possibility that the universe might be subject to a final constraint in addition to the initial Big Bang condition. If both initial and final states of the universe were fixed, then what happens in between could be seen as a kind of globally determined “solution” to a two-point boundary value problem, rather than an initial value (Cauchy) problem. This is reminiscent of the Wheeler-Feynman absorber theory in electrodynamics, where the solution for radiation involves both retarded (forward-in-time) and advanced (backward-in-time) waves, with the condition that all advanced effects cancel except those that fit a future boundary condition (the presence of absorbers) (Retrocausality in Quantum Mechanics) (Backward Causation - Stanford Encyclopedia of Philosophy). In such a picture, the behavior of a particle now could, in principle, depend on conditions in the future (through an advanced influence), meaning the evolution isn’t simply determined by the immediate past state. While Wheeler-Feynman theory was a classical idea and hasn’t become mainstream, its spirit lives on in some interpretations of quantum mechanics that allow future measurements to affect present particle behavior (the two-state vector formalism of Aharonov, for instance, postulates a state vector propagating forward in time and another propagating backward from the future, with physical reality determined by the combination). If something like that were true, the “giant equation” would not be a unilateral time-evolution law but rather a consistency condition linking past and future. The universe would be more like a solved crossword puzzle than a progressing computation – every part interlocks with every other, not derivable by starting at one end alone.

Retrocausality as mentioned before is another non-Markovian concept. If future events can influence the past (in a way that doesn’t create paradoxical loops or violations of macroscopic causality), then the Markov condition is broken – the state at time t plus knowledge of future interventions would predict a different outcome than the state at time t alone. So far, no clear evidence of retrocausality in laboratory physics exists (quantum mechanics is consistent with it in principle but doesn’t demand it). Yet, researchers like Huw Price argue that accepting some backward influence might resolve the tension between quantum mechanics and relativity by allowing a locally causal description at the price of temporal weirdness. From a philosophical standpoint, this reopens the idea that perhaps the division into “cause preceding effect” is a human convention tied to the thermodynamic arrow, and fundamentally, the universe might be permanently holistic, with future and past deeply entwined.

Finally, it’s worth considering that our current notions of time and state may themselves break down at high energies or in quantum gravity. If time is emergent (as some quantum gravity approaches suggest, where at the Planck scale time might not exist as a smooth parameter), then asking if the universe follows a differential equation in time might be like asking if the ocean follows a differential equation in “wave-time” – it might not be the right question at the fundamental level. Instead, the “giant law” of the universe might be something like a principle of extremal information or a holographic condition (as hinted by the holographic principle in quantum gravity) which doesn’t resemble a differential equation in ordinary spacetime at all. Such laws could be inherently non-Markovian when viewed from our emergent time, because they weren’t formulated in that time to begin with.

In these speculative vistas, we see that the Laplacean ideal could fail not only due to indeterminism but due to a need for more than just the immediate past to determine the present. Whether it’s through hidden global variables that correlate everything, or backward-in-time effects, or an atemporal global law, future physics might require relaxing the assumption that the present contains all that is needed to yield the future. If so, the notion of one giant Markovian equation would give way to perhaps a giant non-Markovian structure – maybe an integrodifferential equation with memory, or a two-time boundary condition, or something entirely beyond our current math.

Conclusion

Laplace’s question – is everything that exists encapsulated in one grand formula, evolving inexorably in time? – has driven science for centuries. The Laplacean deterministic paradigm posits a cosmos in which nothing truly novel ever occurs; the future is just the unfolding of the present according to fixed laws. This worldview found early validation in classical physics but encountered headwinds in the 20th century. Quantum mechanics, with its probabilistic outcomes and entangled states, cracked the edifice of determinism and locality. Bell’s theorem drove home that no simple locally Markovian story can account for quantum phenomena (Bell's theorem - Wikipedia) (Bell's theorem - Wikipedia). We either allow nonlocal connections into our “giant equation” or surrender the idea of a precise equation altogether (embracing intrinsic randomness or multiple parallel outcomes). Moreover, the role of causation in physics has been revealed to be subtle: rather than a fundamental force, it appears to be a higher-level descriptor or even an illusion in the fundamental laws (). The march from Newton to Einstein to Feynman to quantum information has been a march away from intuitive mechanism and toward abstract relation – from billiard-ball causality to correlation structures and information.

Is the universe a giant Markovian differential equation? As of 2025, the best answer is: Not in any straightforward sense. If one takes the universal wavefunction in many-worlds, one has an equation (the Schrödinger equation) that is global and deterministic – but it describes a plethora of branching worlds, not a single history, and it raises as many questions as it answers about ontology. If one takes a hidden-variable view like Bohm’s, one restores a single history and determinism, but the price is an interconnection that defies the locality we expect of a Markov process in space, and one might argue that the “giant equation” (Schrödinger + guidance equation) is no longer simple or solely Markovian when considering subsystems. If one takes standard quantum mechanics at face value, the universe is not a single equation but a combination of unitary evolution and probabilistic collapse – a patchwork of law and chance. Increasingly, physicists lean toward frameworks emphasizing conditional probabilities (Bayesian or informational viewpoints) (Path integral formulation - Wikipedia), where the notion of evolving state is secondary to the notion of consistent correlations between preparations and outcomes. This does not necessarily mean physics is giving up on finding a unified description – but it might be that the unified description looks less like “$d\mathbf{x}/dt = F(\mathbf{x})$” and more like a huge probabilistic map, or a network of consistent relationships.

Epistemologically, we have become aware that any “giant equation” might be forever beyond our practical reach – we build effective theories that work at certain scales and circumstances, and each has its own degree of Markovianity or determinism. Metaphysically, the lust for a giant equation is a lust for total intelligibility of the cosmos. Modern physics has shown us glimpses of such intelligibility but also of profound mystery: nonlocal links, uncertain outcomes, possible multiple histories. Perhaps the ultimate truth is a synthesis: a giant equation that is not purely differential in time but rather weaves together space, time, and probability – a “giant algorithm” or principle that when applied, yields the rich tapestry of what we see. Such a principle might make Laplace’s demon smile in recognition yet also concede that Laplace’s own concept was too narrow (too tied to classical clockwork). In conclusion, while the Laplacean ideal of a perfectly deterministic, Markovian universe has been undermined, the search for a unified law of nature continues. It may turn out that all there is can be captured in a single framework – but one that incorporates probabilistic conditionality, nonlocal connectivity, and perhaps a dash of retrocausality or holistic constraint, in order to be consistent with what modern experiments and theories imply about our world (John Stewart Bell) (John Stewart Bell). The universe might not be a simple giant differential equation – but it remains an open question whether it is an elegant “giant something” that future scientists will eventually write on a T-shirt (or more likely, struggle to comprehend even as they write it). For now, Laplace’s legacy survives in our ongoing belief that the universe is ultimately intelligible – even if that intelligibility comes in a form far stranger and less Laplacean than a deterministic Markovian equation.

Sources:

Laplace’s determinism and “demon” (Laplace's demon - Wikipedia)
Russell on eliminability of cause ()
Norton on causation not fundamental ((Microsoft Word - 003004.doc))
Bell’s theorem – no local deterministic theory reproduces QM (Bell's theorem - Wikipedia) (Bell's theorem - Wikipedia)
Bell on nonlocality (Bohm’s model) (John Stewart Bell)
Bell on superdeterminism (predetermined correlations) (John Stewart Bell)
Path integral viewpoint – physics as $P(B|A)$ (Path integral formulation - Wikipedia)
Path integral normalization (universal state as after Big Bang) (Path integral formulation - Wikipedia)
Bell on retrocausality proposals (Price, etc.) https://www.informationphilosopher.com/solutions/scientists/bell/#:~:text=Following%20John%20Bell%27s%20idea%2C%20Nicholas,as%20has%20philosopher%20%20697

Inspiration

The Most Overlooked Idea in Quantum Physics

AI Reasoning

the only question that can be asked in physics is: What fraction of states satisfying condition A also satisfy condition B?

I'm thinking through Laplace's deterministic view, quantum nonlocality, path integrals, and emergent causation. Shifting to conditional probabilities, I consider the epistemological and metaphysical implications.

I’m thinking about non-Markovian global constraints, retrocausality, and interpretations of quantum mechanics like the Wheeler-Feynman absorber theory and transactional interpretation. Global consistency in quantum mechanics seems intriguing.

I'm checking the screenshot for text about path integral.

I’m looking into embedding the image to understand the content.

Mapping out the path integral formulation Wikipedia image and transcript, considering browser methods to view the image.

Searched for Russell Bell Norton transcriptChatGPT

I'm analyzing steps like searching the web or checking separate contexts for "Russell Bell Norton Laplace giant Markovian differential equation" to locate the transcript.

Searched for Laplace Markovian differential equation transcriptChatGPT

Piecing together Russell's causality, Bell's theorem implications, and Norton's causation arguments.

I'm evaluating how causality fits into quantum mechanics, considering deterministic and probabilistic views, and exploring global constraints and non-Markovian concepts. But what if these models just scratch the surface?

I’m digging into philosophical views like Laplace's demon, Russell on causation, Bell's theorem, and Reichenbach's principle of common cause. Progressing through causation's role and implications.

I'm looking into the "Path integral formulation" on Wikipedia to better understand its application.

Searched for conditional probability P(B|A)ChatGPT

OK, let me see. The image might be of a formula or text, but I’m not sure which.

Searched for conditional probability P(B|A) path integral WikipediaChatGPT

I’m piecing together a solution to pinpoint a specific Wikipedia snippet by using the browser.open function with a path integral page id. This approach seems more direct.

Searched for path integral formulation Wikipedia P(B|A)ChatGPT

I'm looking at the use of path integrals in quantum mechanics, which employ formal analogies.

Path integrals apply formal analogies to quantum mechanics, linking classical actions to probability amplitudes.

Read en.wikipedia.org

ChatGPT

I'm curious if the screenshot shows an image from a Wiki, possibly labeled P(B|A) or similar, potentially as a caption or figure.

Is Causation Doomed?

Table of Contents

Introduction

Laplace’s Deterministic Vision and the Markovian Paradigm

Quantum Mechanics: Indeterminism and Nonlocality

Is Causation Fundamental? The Russellian Challenge

The Path Integral: Histories and Conditional Probabilities

From Equations to Information: Shifting Paradigms

Beyond Markovian Equations: Global Constraints and Retrocausality

Conclusion

Inspiration

The Most Overlooked Idea in Quantum Physics

AI Reasoning

Comments

Latest

Donald D. Hoffman: Perceived "Reality" is an evolved user interface tuned for Fitness, not Truth.

Is Reality a Construction of the Self: Frauchiger–Renner Paradox Quantum-Philosophical Perspective

Who Are We? Emergent Intelligence in LLMs - Parallels between human and artificial cognition

Understanding Adam and Eve in the Garden of Eden - one of the most enduring myths in human culture

Is Causation Doomed?

Table of Contents

Introduction

Laplace’s Deterministic Vision and the Markovian Paradigm

Quantum Mechanics: Indeterminism and Nonlocality

Is Causation Fundamental? The Russellian Challenge

The Path Integral: Histories and Conditional Probabilities

From Equations to Information: Shifting Paradigms

Beyond Markovian Equations: Global Constraints and Retrocausality

Conclusion

Inspiration

The Most Overlooked Idea in Quantum Physics

AI Reasoning

Comments

Related

Latest